 por Ovelha » Qua Nov 27, 2013 13:03
por Ovelha » Qua Nov 27, 2013 13:03
conituando topico anterior tem mais essa
Se A

B=

então A


=A
Seja x

(A

B)=


x

A e x

B
x

(A

B)=


x

A e x e x

B. Daí x

(A

B) e x

(A

B). Contradição
Agradeço desde já a compreensão e ajuda de todos
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
 por e8group » Qua Nov 27, 2013 14:30
por e8group » Qua Nov 27, 2013 14:30
Na minha opinião ,novamente você errou no inicio em dizer que " seja

" . Ora , se por hipótese
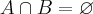
então não podemos ter

pertencendo a este conjunto .
Tenho uma dica :
Trivialmente
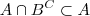
, então basta mostra que
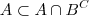
para concluir que

.
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ovelha » Qua Nov 27, 2013 16:13
por Ovelha » Qua Nov 27, 2013 16:13
Olá. No caso dessa questão eu já havia entendido a interseção não daria certo apenas mostrei que seria contradição dizer isso a ideia era mostra a contradição então peço que mostre como ficaria o que vc está falando.
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
 por e8group » Qua Nov 27, 2013 16:33
por e8group » Qua Nov 27, 2013 16:33
OK . Vamos tentar .
Dado

em

,temos que

não pertence a

(pois por hipótese
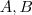
são disjuntos ) . Desta forma, concluímos que

pertence a interseção de

com
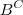
e como

é genérico, mostramos
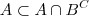
e assim o resultado segue .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ovelha » Qua Nov 27, 2013 16:41
por Ovelha » Qua Nov 27, 2013 16:41
Obrigado
-
Ovelha
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Nov 13, 2013 11:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em física
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstração de conjnuntos
por Ovelha » Qua Nov 27, 2013 17:41
- 2 Respostas
- 1283 Exibições
- Última mensagem por Ovelha

Qui Nov 28, 2013 12:49
Conjuntos
-
- DEMONSTRAÇÃO
por arima » Seg Nov 08, 2010 08:40
- 8 Respostas
- 5915 Exibições
- Última mensagem por roseli

Qua Nov 10, 2010 21:03
Álgebra Elementar
-
- Demonstração
por Lorettto » Qui Dez 16, 2010 23:03
- 3 Respostas
- 2268 Exibições
- Última mensagem por Elcioschin

Seg Dez 20, 2010 12:39
Álgebra Elementar
-
- Demonstração
por Pedro2 » Sáb Mar 12, 2011 15:38
- 1 Respostas
- 1953 Exibições
- Última mensagem por Guill

Sex Abr 20, 2012 16:01
Matrizes e Determinantes
-
- PA - Demonstração
por jessicaccs » Sex Mar 25, 2011 11:52
- 1 Respostas
- 1468 Exibições
- Última mensagem por Elcioschin

Sex Mar 25, 2011 14:55
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 B=
B= então A
então A 
 =A
=A (A
(A  B)=
B)=
 x
x  A e x
A e x  B
B (A
(A  B)=
B)=
 x
x  A e x e x
A e x e x  B. Daí x
B. Daí x  (A
(A  B) e x
B) e x  (A
(A  B). Contradição
B). Contradição
 B=
B= então A
então A 
 =A
=A (A
(A  B)=
B)=
 x
x  A e x
A e x  B
B (A
(A  B)=
B)=
 x
x  A e x e x
A e x e x  B. Daí x
B. Daí x  (A
(A  B) e x
B) e x  (A
(A  B). Contradição
B). Contradição
 " . Ora , se por hipótese
" . Ora , se por hipótese 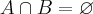 então não podemos ter
então não podemos ter  pertencendo a este conjunto .
pertencendo a este conjunto .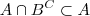 , então basta mostra que
, então basta mostra que 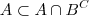 para concluir que
para concluir que  .
. 

 em
em  ,temos que
,temos que  não pertence a
não pertence a  (pois por hipótese
(pois por hipótese 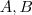 são disjuntos ) . Desta forma, concluímos que
são disjuntos ) . Desta forma, concluímos que  pertence a interseção de
pertence a interseção de  com
com 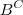 e como
e como  é genérico, mostramos
é genérico, mostramos 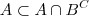 e assim o resultado segue .
e assim o resultado segue .

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
