Olá a todos,
Não consegui resolver o problema abaixo. Do livro de Gelson Iezzi, pág. 16.
Se puderem me ajudar agradeceria muito,
http://img144.imagevenue.com/img.php?im ... _182lo.jpg
Obrigado
-------------------Depois de postar, li, e postei...
Bom, fui ler as recomendações depois de ter postado.
Fiz tentativas sim de resolver o problema. Vou tentar colocar aqui. Ainda não sei como... Vou pesquisar...
De qualquer modo obrigado.
-------------
Tentando me explicar.
Primeiro peguei a dizima periódica 7,3636363636... e transformei numa fração.
Fiz 7,363636... = w
Fiz 736,363636.....= 100w
Depois subtrai uma da outra.
Ficou 729=99w
w ficou aquela divisao. 729 por 99.
Simplifiquei e obtive 81/11
OK
-----------
Depois x/y resulta em um quociente z com resto 8.
Fiz: zy+8=x
-----------
no fim não dá......... z fica racional



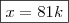 e
e  .
.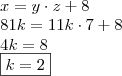
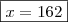 e
e  .
.
