Olá, tentei ler a teoria pelo liro e fiquei meio confuso, acabei nao conseguindo resolver esse exercicio, quem puder me ajudar:
É numero real ? Justifique sua resposta.
a(alfa) = {p E(pertence) Q | 3p + 1< 2p - 5}
quem puder me ajudar, grato desde já.


 ,de números racionais ,que satisfaz 4 propriedades .
,de números racionais ,que satisfaz 4 propriedades . e
e  é um número racional com
é um número racional com 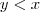 ,então
,então 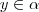 .
. 
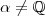
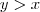 .
. ,temos :
,temos :  racionais quaisquer , com
racionais quaisquer , com  e
e 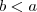 ,temos :
,temos : .
.  implica que
implica que 

 e
e