 por JKS » Sáb Ago 25, 2012 04:38
por JKS » Sáb Ago 25, 2012 04:38
Preciso de ajuda, desde já agradeço.
(PUC) Seja f(x) =

a) Determine as soluções de f(x)=x (consegui fazer)
b) Determine para quais valores do parâmetro real m a equação f(x)=x+m admite solução real.(não entendi)
c) Seja g(x) = f(f(x)). Determine os valores de x para os quais g(x)
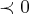
(não consegui)
Resposta : b)
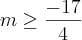
c)
![- \sqrt[]{6}\prec x \prec -\sqrt[]{2}... ou... \sqrt[]{2}\precx\prec\sqrt[]{6} - \sqrt[]{6}\prec x \prec -\sqrt[]{2}... ou... \sqrt[]{2}\precx\prec\sqrt[]{6}](/latexrender/pictures/4645ff90ecd77d3f5cf9930cbdfa846c.png)
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Ago 25, 2012 10:36
por MarceloFantini » Sáb Ago 25, 2012 10:36
Para o item (b) faça

, daí
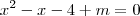
. Para que isto tenha soluções devemos ter
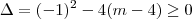
. Encontre os valores de

que satisfazem a desigualdade.
Para o item (c), note que pela composição de funções temos que
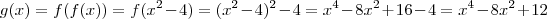
. Faça a mudança de variável

e analise o sinal, voltando pra variável original depois e continuando.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [função](UFF-NÃO ESPECÍFICA)
por JKS » Qui Ago 23, 2012 19:07
- 2 Respostas
- 1020 Exibições
- Última mensagem por JKS

Sex Ago 24, 2012 12:44
Funções
-
- [função quadrática] UFF ESPECÍFICA
por JKS » Sex Ago 24, 2012 13:34
- 1 Respostas
- 1025 Exibições
- Última mensagem por fraol

Qui Ago 30, 2012 23:29
Funções
-
- [números complexos] ESPECÍFICA
por JKS » Dom Set 23, 2012 01:15
- 1 Respostas
- 2633 Exibições
- Última mensagem por MarceloFantini

Dom Set 23, 2012 02:03
Números Complexos
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5583 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

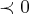 (não consegui)
(não consegui)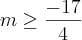
![- \sqrt[]{6}\prec x \prec -\sqrt[]{2}... ou... \sqrt[]{2}\precx\prec\sqrt[]{6} - \sqrt[]{6}\prec x \prec -\sqrt[]{2}... ou... \sqrt[]{2}\precx\prec\sqrt[]{6}](/latexrender/pictures/4645ff90ecd77d3f5cf9930cbdfa846c.png)


 , daí
, daí 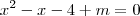 . Para que isto tenha soluções devemos ter
. Para que isto tenha soluções devemos ter 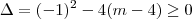 . Encontre os valores de
. Encontre os valores de  que satisfazem a desigualdade.
que satisfazem a desigualdade.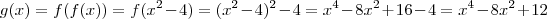 . Faça a mudança de variável
. Faça a mudança de variável  e analise o sinal, voltando pra variável original depois e continuando.
e analise o sinal, voltando pra variável original depois e continuando.



 , avisa que eu resolvo.
, avisa que eu resolvo.

