Obrigado. Creio que o último -1 não faz parte, correto?
Resolução

Por se tratar de uma soma/subtração de frações em ambos os lados da equação, precisaremos tirar o MMC (Mínimo Múltiplo Comum) para podermos efetuar a soma/subtração dos numeradores.
O Mínimo Múltiplo Comum (MMC) entre (3x - 1) e (3x + 1), na parte esquerda da equação é: (3x - 1)(3x + 1) e do lado direito da equação, o MMC entre (9x^2 - 1) e 1 é (9x^2 -1).
Dividindo-se cada MMC de cada lado por cada um dos denominadores e multiplicando-se pelo seus numeradores teremos: (Exemplo: (3x - 1)(3x + 1) dividido por (3x - 1) e multiplicando-se por 2, ficará 2(3x + 1) = 6x + 2 e dividindo-se (3x - 1)(3x + 1) por (3x + 1) e multiplicando-se por 3x teremos: 3x(3x - 1) = 9x^2 - 3x. Por fim, no lado esquerdo ainda, pegamos estes dois resultados e teremos 6x + 2 - (9x^2 - 3x) no numerador, ou seja, 6x + 2 - 9x^2 + 3x), como mostrado abaixo:
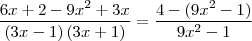

Como: 9x^2 - 1 está divindo no lado esquerdo da equação, passarei para o lado direito multiplicando. Temos então:
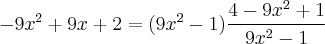
Efetuando a divisão no lado direito da equação, ficaremos finalmente com:
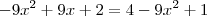
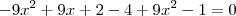
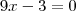
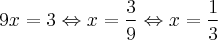

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



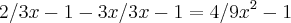

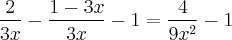




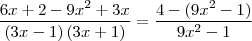

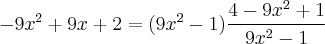
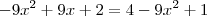
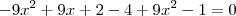
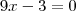
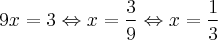


 faz parte sim e com relação a essa resolução, nao entendi como você chegou ao Raciocínio da Segunda linha
faz parte sim e com relação a essa resolução, nao entendi como você chegou ao Raciocínio da Segunda linha
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)