 por lucasmatematico » Qua Jun 10, 2015 23:31
por lucasmatematico » Qua Jun 10, 2015 23:31
QUESTÃO 1: O leitor está trabalhando no departamento de marketing de urna companhia de Software. Sua equipe de vendas verifica que é possível vender em um ano um máximo de 30.000
·unidades de um novo produto. O leitor fórmula a hipótese de que a taxa de crescimento das vendas x
- seja proporcional à diferença entre a venda máxima e a vencia atual. Determine uma solução geral.
QUALQUER AJUDA SERVE.
-
lucasmatematico
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 10, 2015 23:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por nakagumahissao » Seg Out 05, 2015 12:07
por nakagumahissao » Seg Out 05, 2015 12:07
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações Diferencias Ordinárias- Urgente
 por leroaquino » Sáb Set 19, 2015 14:17
por leroaquino » Sáb Set 19, 2015 14:17
- 0 Respostas
- 1373 Exibições
- Última mensagem por leroaquino

Sáb Set 19, 2015 14:17
Equações
-
- Equações Diferencias
por Arthur Bruno » Sex Nov 04, 2016 00:46
- 1 Respostas
- 1441 Exibições
- Última mensagem por adauto martins

Seg Nov 07, 2016 10:07
Cálculo: Limites, Derivadas e Integrais
-
- Equações Diferencias Ordinários
 por leroaquino » Ter Set 22, 2015 21:10
por leroaquino » Ter Set 22, 2015 21:10
- 1 Respostas
- 1956 Exibições
- Última mensagem por adauto martins

Dom Set 27, 2015 12:34
Equações
-
- [EQUAÇÕES DIFERENCIAIS ORDINÁRIAS]
por NavegantePI » Qui Mar 02, 2017 00:43
- 0 Respostas
- 6288 Exibições
- Última mensagem por NavegantePI

Qui Mar 02, 2017 00:43
Equações
-
- Livro EDO: Introdução às Equações Diferenciais Ordinárias
 por admin » Sáb Jul 21, 2007 19:59
por admin » Sáb Jul 21, 2007 19:59
- 2 Respostas
- 6097 Exibições
- Última mensagem por bruno_dias

Ter Set 01, 2009 01:54
Cálculo
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


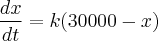

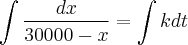


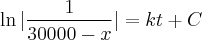

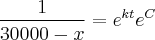

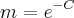
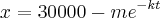


 .
.



