 por RodriguesBruno » Qui Mai 29, 2014 10:08
por RodriguesBruno » Qui Mai 29, 2014 10:08
Olá
Primeiramente, não tenho muita certeza se estou postando a pergunta na categoria certa, então peço desculpas se estiver enganado, mas, de qualquer forma, queria que alguém me desse uma ajuda.
Fiz um concurso no domingo e tinha a seguinte questão:
Assinale a alternativa FALSA.
a.
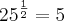
b.
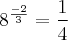
c.
![{3}^{\frac{1}{4}}.3=\sqrt[]{3}} {3}^{\frac{1}{4}}.3=\sqrt[]{3}}](/latexrender/pictures/09f482fe34278a38199825534df76d94.png)
d.
![\frac{2}{\sqrt[]{2}}}=\sqrt[]{2}} \frac{2}{\sqrt[]{2}}}=\sqrt[]{2}}](/latexrender/pictures/afd62a6225fa52600c594549d8a2135d.png)
Minha resposta foi a letra C, porém o gabarito mostra como correta a
letra A.
Fazendo a conta,
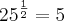
se torna
![\sqrt[2]{25} \sqrt[2]{25}](/latexrender/pictures/e4a5a0d745e039d5327ad2983233661c.png)
que é igual a 5, como indicado na alternativa, portanto, esta seria verdadeira e não falsa como o pede o comando da questão. Queria pedir para que alguém possa me esclarecer, o gabarito está mesmo incorreto?
Obs.: Tenho outra questão em aberto sobre esse mesmo concurso. Peço que se puderem, deem uma olhada e vejam se podem me ajudar.
(viewtopic.php?f=119&t=14251&p=46686&hilit=geometria+trigonometria#p46686)Desde já agradeço.
Bruno
-
RodriguesBruno
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 20, 2014 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Sex Mai 30, 2014 00:21
por Russman » Sex Mai 30, 2014 00:21
Certamente a alternativa falsa é a c.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por RodriguesBruno » Sex Mai 30, 2014 16:32
por RodriguesBruno » Sex Mai 30, 2014 16:32
Russman escreveu:Certamente a alternativa falsa é a c.
Ainda bem, porque por um minuto fiquei preocupado com a questão, refiz todas as alternativas, cheguei a mesma conclusão. Agora com sua confirmação, fico mais tranquilo e posso entrar com um recurso sobre a questão.
Fico muito agradecido
-
RodriguesBruno
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 20, 2014 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3153 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4149 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3427 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equações
por Neperiano » Qua Fev 11, 2009 12:33
- 6 Respostas
- 6491 Exibições
- Última mensagem por marcio silva

Sex Mar 20, 2009 20:15
Sistemas de Equações
-
- Equações
por Luna » Qui Set 10, 2009 19:30
- 2 Respostas
- 2267 Exibições
- Última mensagem por Luna

Sex Set 11, 2009 19:54
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
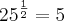
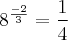
![{3}^{\frac{1}{4}}.3=\sqrt[]{3}} {3}^{\frac{1}{4}}.3=\sqrt[]{3}}](/latexrender/pictures/09f482fe34278a38199825534df76d94.png)
![\frac{2}{\sqrt[]{2}}}=\sqrt[]{2}} \frac{2}{\sqrt[]{2}}}=\sqrt[]{2}}](/latexrender/pictures/afd62a6225fa52600c594549d8a2135d.png)
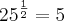 se torna
se torna ![\sqrt[2]{25} \sqrt[2]{25}](/latexrender/pictures/e4a5a0d745e039d5327ad2983233661c.png) que é igual a 5, como indicado na alternativa, portanto, esta seria verdadeira e não falsa como o pede o comando da questão. Queria pedir para que alguém possa me esclarecer, o gabarito está mesmo incorreto?
que é igual a 5, como indicado na alternativa, portanto, esta seria verdadeira e não falsa como o pede o comando da questão. Queria pedir para que alguém possa me esclarecer, o gabarito está mesmo incorreto?


