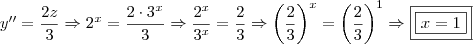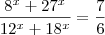
Tentei resolver da seguinte forma:

* Fazendo 2^x = y, e 3^x = z
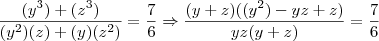
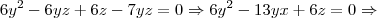
Resolvendo a equação do 2° grau em função de y, obtemos: y' = 9z, e y'' = 4z
Tentei resolver, usando esses valores, para resolver a equação exponencial e encontrei valores estranhos, sem sentido
* Por exemplo, no 1° caso, para y=9z >>> z = 0 (y = 0) e >>>> 3^x = 0, onde x real não existe.
* No 2° caso, para y = 4z >>>> obtenho uma equação que não possui resultado (sentença impossível).
Será que alguém poderia me ajudar, e me dar uma sugestão para que eu consiga resolver esse problema ?


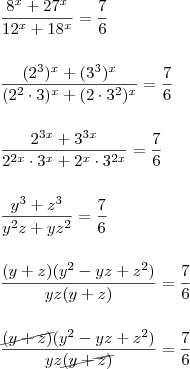

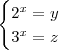 , então, encontremos o valor de
, então, encontremos o valor de  usando a raiz
usando a raiz  ;
;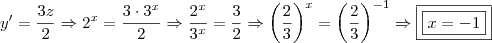
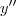 ;
;