 por Thiago 86 » Ter Mar 12, 2013 15:00
por Thiago 86 » Ter Mar 12, 2013 15:00
Saldações

, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
Para que valores de "m" a equação

, admite raizes reais simétricas.
1° dúvida. O termo simetria usado, significa igualdade?
Como eu tentei:
![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Ter Mar 12, 2013 16:49
por Russman » Ter Mar 12, 2013 16:49
Não! Números simétricos tem o mesmo módulo, mas sinais opostos. O simétrico de

é

.
Assim, as raízes da equação tem de ser

e
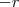
. Há diversas formas de resolver essa questão. Optei por esta:
A equação tem raízes

e
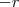
. Assim, podemos escreve-la como

de forma que
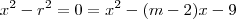
.
Por igualdade de polinômios, temos, então
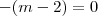
, de onde
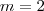
, e

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Thiago 86 » Qua Mar 13, 2013 09:39
por Thiago 86 » Qua Mar 13, 2013 09:39
Saudações

.
Descupe-me, mas eu não sei o que é números simétricose.
Eu estou estudando matemática sozinho, desde o início com uma apostila, e estou vendo que ela tem algumas falhas se você tivesse algum material falando sobrre simetria que pudece me enviar ficaria agradecido.
Voltando para a questão, é por isso que eu não consegui entender porque x=-x.
Desde já muito obrigado.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
Voltar para Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando. , admite raizes reais simétricas.
, admite raizes reais simétricas.![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)

 , estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando. , admite raizes reais simétricas.
, admite raizes reais simétricas.![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)

 é
é  .
. e
e 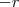 . Há diversas formas de resolver essa questão. Optei por esta:
. Há diversas formas de resolver essa questão. Optei por esta: e
e 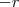 . Assim, podemos escreve-la como
. Assim, podemos escreve-la como
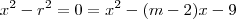 .
.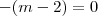 , de onde
, de onde 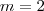 , e
, e  .
.
 .
.