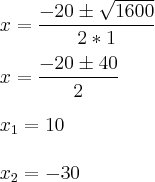por matemarcos » Qua Abr 18, 2018 22:38
por matemarcos » Qua Abr 18, 2018 22:38
Acostumado a resolver apenas questões que envolve o x e o y do vértice Travei nessa questão. Agradeço quem puder me ajudar.
Considere que uma indústria farmacêutica tem sua produção diária P, em caixas de
remédios, variando com o número de funcionários x, de acordo com a função
P(x) = x² + 20x + 700, para x ? 5. Para produzir 1.000 caixas de remédios, a quantidade
necessária de funcionários é de
A) 12. C) 14.
B) 10. D) 16.
-
matemarcos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jan 11, 2018 22:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Informática
- Andamento: formado
 por Gebe » Qua Abr 18, 2018 22:54
por Gebe » Qua Abr 18, 2018 22:54
matemarcos escreveu:Acostumado a resolver apenas questões que envolve o x e o y do vértice Travei nessa questão. Agradeço quem puder me ajudar.
Considere que uma indústria farmacêutica tem sua produção diária P, em caixas de
remédios, variando com o número de funcionários x, de acordo com a função
P(x) = x² + 20x + 700, para x ? 5. Para produzir 1.000 caixas de remédios, a quantidade
necessária de funcionários é de
A) 12. C) 14.
B) 10. D) 16.
Como mencionado no enunciado P é a produção de caixas de remedios e x o n° de funionarios.
Queremos saber o numero de funcionarios (x) para uma produção de 1000 caixas (P)
Substituindo o "P" dado, temos:
1000 = x² + 20x + 700
Reorganizando...
x² + 20x - 300 = 0
Agora bsta utilizarmos Bhaskara:
Delta: 20² - 4*1*(-300) = 1600
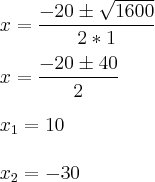
Como não podemos ter numero de funcionarios (x) negativo, o valor correto é 10 funcionarios (letraB).
Espero ter ajudado, boons estudos.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] alguem sabe resolver essa expressão?
por tainaraabp » Ter Out 02, 2012 11:35
- 1 Respostas
- 2062 Exibições
- Última mensagem por LuizAquino

Ter Out 02, 2012 12:25
Cálculo: Limites, Derivadas e Integrais
-
- quem pode me ajudar a resolver essa equaçao?obrigado!
por flavio970 » Qua Set 30, 2015 16:10
- 1 Respostas
- 2116 Exibições
- Última mensagem por nakagumahissao

Qua Set 30, 2015 20:15
Equações
-
- Por favor alguém sabe resolver esta questão
por costav13 » Sáb Nov 09, 2013 10:10
- 3 Respostas
- 2578 Exibições
- Última mensagem por e8group

Dom Nov 10, 2013 13:29
Cálculo: Limites, Derivadas e Integrais
-
- Pra quem sabe !!
por brunox1x » Dom Jun 16, 2013 15:33
- 1 Respostas
- 3940 Exibições
- Última mensagem por DanielFerreira

Ter Fev 18, 2014 09:28
Desafios Fáceis
-
- Facil Pra quem sabe !!
por brunox1x » Dom Jun 16, 2013 15:35
- 1 Respostas
- 1710 Exibições
- Última mensagem por timoteo

Dom Jun 16, 2013 16:07
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.