 por adauto martins » Dom Set 27, 2015 12:34
por adauto martins » Dom Set 27, 2015 12:34
a)

...faz-se
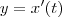
,teremos p/
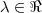
,fazendo
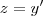
,teremos:
![dz/dx=(dz/dy).(dy/dx) \Rightarrow f(t,x,y)=z.dz/dy [\tex]
[tex]\int_{z}^{{z}_{0}}dz=\int_{y}^{{y}_{0}}(f(...)/z)dy dz/dx=(dz/dy).(dy/dx) \Rightarrow f(t,x,y)=z.dz/dy [\tex]
[tex]\int_{z}^{{z}_{0}}dz=\int_{y}^{{y}_{0}}(f(...)/z)dy](/latexrender/pictures/435d4aba7c4c538248bbe738e22472ac.png)
...
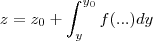
...
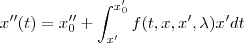
...
ps-esse editor esta muito ruim de trabalhar,mas é por ai...espero q. entenda...e ir parametrizando,reduzindo o grau e resolvendo as integrais...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações Diferencias
por Arthur Bruno » Sex Nov 04, 2016 00:46
- 1 Respostas
- 1441 Exibições
- Última mensagem por adauto martins

Seg Nov 07, 2016 10:07
Cálculo: Limites, Derivadas e Integrais
-
- Equações Diferencias Ordinárias- Urgente
 por leroaquino » Sáb Set 19, 2015 14:17
por leroaquino » Sáb Set 19, 2015 14:17
- 0 Respostas
- 1373 Exibições
- Última mensagem por leroaquino

Sáb Set 19, 2015 14:17
Equações
-
- [DUVIDA EM EQUAÇOES DIFERENCIAS ORDINARIAS]
por lucasmatematico » Qua Jun 10, 2015 23:31
- 1 Respostas
- 1649 Exibições
- Última mensagem por nakagumahissao

Seg Out 05, 2015 12:07
Equações
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3153 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4147 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ...faz-se
...faz-se 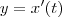 ,teremos p/
,teremos p/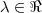 ,fazendo
,fazendo 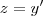 ,teremos:
,teremos:![dz/dx=(dz/dy).(dy/dx) \Rightarrow f(t,x,y)=z.dz/dy [\tex]
[tex]\int_{z}^{{z}_{0}}dz=\int_{y}^{{y}_{0}}(f(...)/z)dy dz/dx=(dz/dy).(dy/dx) \Rightarrow f(t,x,y)=z.dz/dy [\tex]
[tex]\int_{z}^{{z}_{0}}dz=\int_{y}^{{y}_{0}}(f(...)/z)dy](/latexrender/pictures/435d4aba7c4c538248bbe738e22472ac.png) ...
...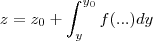 ...
...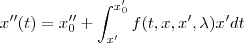 ...
...

 .
.
 :
: