quando tem isso:

não sei se o
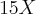 vai na frente ou atrás do
vai na frente ou atrás do 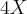 .
.Outro exemplo:
 , nesse caso nao sei se o
, nesse caso nao sei se o  vai na frente ou atrás do
vai na frente ou atrás do  . Olha como ficaria a minha:
. Olha como ficaria a minha:9X+3=2X
9X-2X=-3
7X=-3
X=
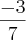
e a primeira:
4X-4=15X+3
nessa eu coloco o 15X na frente do 4X , sendo que na outra eu coloquei o n° que passava , atrás , errado?
15X-4X=3+4
11X=7

Por favor me tirem essa dúvida





 e também
e também  ou
ou  .
.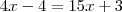 . Somando
. Somando 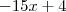 dos dois lados segue
dos dois lados segue  , que resulta em
, que resulta em  e portanto
e portanto 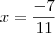 .
. para anular
para anular 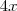 à esquerda e
à esquerda e  à direita e chegaria na mesma resposta.
à direita e chegaria na mesma resposta.


 , avisa que eu resolvo.
, avisa que eu resolvo.

