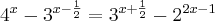
S={3/2}
Galera, eu tentei transformar em bases iguais e depois colocar as bases ''3'' de um lado, e as bases ''2'' do outro, e a partir daí colocar em evidência, mas eu n sei como igualar ja que de um lado é 3 e do outro 2.. enfim to meio perdido, se além de resolverem puderem explicar como fizeram ficarei muito grato ^^
Bruno lima.


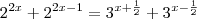 (basta somar nos dois lados da igualdade
(basta somar nos dois lados da igualdade 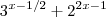 e utilizar
e utilizar 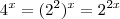 )
) 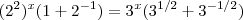 .
.
![2^{2x}(\frac{3}{2})=3^x(\frac{4\sqrt[2]{3}}{3}) 2^{2x}(\frac{3}{2})=3^x(\frac{4\sqrt[2]{3}}{3})](/latexrender/pictures/b6480063a63d2f8a501168dc85ee26c8.png)
 (poderia também ser 2^(2x)) vamos obter
(poderia também ser 2^(2x)) vamos obter 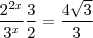 , façamos o mesmo com
, façamos o mesmo com 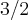 obtendo
obtendo 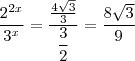 . Agora note que ao invés escrever
. Agora note que ao invés escrever 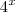 como
como 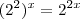 (mencionado esta propriedade no primeiro post ) vamos fazer o contrário para utilizar a seguinte propriedade
(mencionado esta propriedade no primeiro post ) vamos fazer o contrário para utilizar a seguinte propriedade 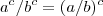 .
. 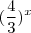 ,portanto
,portanto 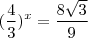 .Mas
.Mas 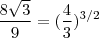 (Fica como exercício ) , então
(Fica como exercício ) , então 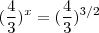 . Logo
. Logo 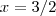 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)