por Amandatkm » Qui Mai 02, 2013 18:36
por Russman » Qui Mai 02, 2013 23:24
. No 1° shopping ele gastou metade do que tinha, ou seja, gastou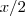 
. No segundo também, ou seja, 
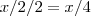. No 3° 
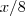e no 4° 
. Ainda gastou 
reais de estacionamento. Portanto, o que ele tinha menos o que ele gastou deve ser os 8 reais que lhe sobraram. 
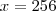que não está nas alternativas. ;/
por e8group » Sex Mai 03, 2013 12:49
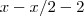.Neste contexto , o sujeito gastará 
reais na segunda compra , e por conseguinte , o dinheiro disponível após esta compra será ![(x - x/2 - 2 ) - [(x - x/2 - 2)/2 - 2]](/latexrender/pictures/1011f756bbb8127cdfa59facbf941e06.png "(x - x/2 - 2 ) - [(x - x/2 - 2)/2 - 2]")
;logo ná próxima compra o sujeito gastará metade deste dinheiro + 2,00 reais com estacionamento .O raciocínio em diante é semelhante .Talvez seja desnecessário , mas poderíamos estender o limite de compras para algum 
natural qualquer tal que o saldo disponível para as próximas compras não seja negativo .Com efeito de computar o dinheiro após as compras ,apresento a vocês a função ![C : \{0,\hdots ,n\} \mapsto [x,0] (x>0)](/latexrender/pictures/588254622c5043abc2a52ee4f0deebe8.png "C : \{0,\hdots ,n\} \mapsto [x,0] (x>0)")
, ou melhor, poderemos provar por indução que após a 
-ésima compra o dinheiro disponível será ![C(k) = \frac{x-4[2^k-1]}{2^k} ; k \in \{0,\hdots ,n\}](/latexrender/pictures/e187a554243f6dc22b0e0edec4b7c4bf.png "C(k) = \frac{x-4[2^k-1]}{2^k} ; k \in \{0,\hdots ,n\}")
.Assim ,tomando-se
, podemos notar que após a 4-ésima compra , o dinheiro disponível será![C(4) = \frac{x -4[2^4-1]}{2^4} = \frac{x -60}{16}](/latexrender/pictures/b64bba38f0959cf1a0c402fd1bf34a79.png "C(4) = \frac{x -4[2^4-1]}{2^4} = \frac{x -60}{16}")
.Por outro lado ,foi dado que o dinheiro disponível após a quarta compra corresponde a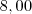 
reais . 
.Resolvendo a equação encontrará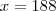 
reais .Apesar da resposta está em uma das alternativas ,há possibilidades de conclusões erradas .por Amandatkm » Sex Mai 03, 2013 18:37
por e8group » Sex Mai 03, 2013 19:13
reais (vou incluir vc na história ) . Após a primeira compra (feita no primeiro shopping) você gastou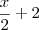 
reais (2 reais referente ao estacionamento) , logo após este evento vc não tem mais reais e sim 
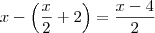reais . Assim , na segunda compra você gastou 
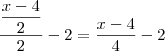reais , e portanto o dinheiro que você terá após este evento será 
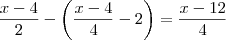reais . O raciocínio em diante é semelhante . Comente as dúvidas ..por Amandatkm » Sex Mai 03, 2013 19:22
por e8group » Sáb Mai 04, 2013 02:33
.por Amandatkm » Sáb Mai 04, 2013 13:39
por e8group » Sáb Mai 04, 2013 14:35
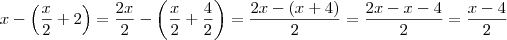. Deixando todos números em mesmo denominador , segue 
. Este valor corresponde ao gasto no terceiro shopping .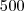
reais reais no primeiro shopping + uma taxa de 2 reais com o estacionamento ,você terá ainda 
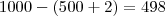reais para gastar com suas compras . Se no segundo Shopping você gastou metade deste dinheiro + 2 reais com estacionamento ,isto é , 
reais .Então você possuirá 
reais para continuar comprando .E assim sucessivamente ,a cada compra você gastará metade do valor disponível + 2 reais com estacionamento .por Amandatkm » Dom Mai 05, 2013 13:47
por e8group » Dom Mai 05, 2013 13:58
. 
. por e8group » Dom Mai 05, 2013 14:01
por Amandatkm » Dom Mai 05, 2013 14:05
por e8group » Dom Mai 05, 2013 14:23
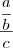Amandatkm escreveu:coloca o codigo : \frac{a}{b} mas os dois numeros é?
são apenas números arbitrários(claro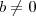 
,mas esta análise não convém neste momento ) ;estou apenas mostrando o código que gera a divisão de dois números em LaTeX . [tex] \frac{x-4}{2}[/tex] 
por boskim22 » Sex Jun 03, 2011 16:46
por pegr » Sáb Jun 08, 2013 01:09
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes