 , estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.Para que valores de "m" a equação
 , admite raizes reais simétricas.
, admite raizes reais simétricas.1° dúvida. O termo simetria usado, significa igualdade?
Como eu tentei:
![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)

 , estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando. , admite raizes reais simétricas.
, admite raizes reais simétricas.![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)

 é
é  .
. e
e 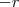 . Há diversas formas de resolver essa questão. Optei por esta:
. Há diversas formas de resolver essa questão. Optei por esta: e
e 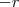 . Assim, podemos escreve-la como
. Assim, podemos escreve-la como
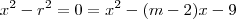 .
.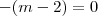 , de onde
, de onde 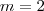 , e
, e  .
.
 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: