 por Gustavo Gomes » Qui Jan 31, 2013 22:03
por Gustavo Gomes » Qui Jan 31, 2013 22:03
Olá, pessoal.
Calculei as raízes da seguinte equação:
![\sqrt[]{3x-2}=\sqrt[]{x} + 2 \sqrt[]{3x-2}=\sqrt[]{x} + 2](/latexrender/pictures/9ab84a666b2608567531a7a3bfdd70e7.png)
:
![{\left(\sqrt[]{3x-2} \right)}^{2}={\left(\sqrt[]{x}+2 \right)}^{2}\Rightarrow{x}^{2}-10x+9=0 {\left(\sqrt[]{3x-2} \right)}^{2}={\left(\sqrt[]{x}+2 \right)}^{2}\Rightarrow{x}^{2}-10x+9=0](/latexrender/pictures/c8cdbe689fd85da2ea25a208180628de.png)
Desse modo, as raízes reais seriam 9 e 1. No entanto, a equação não é satisfeita para x = 1.
Não entendi porque o 1 não corresponde à raiz real da referida equação.....
Aguardo. Grato.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por DanielFerreira » Qui Jan 31, 2013 22:26
por DanielFerreira » Qui Jan 31, 2013 22:26
Gustavo,
deverás substituir os valores de

que encontraste na equação inicial, isto é, substituir

e
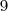
em
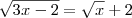
, e, verificar se é verdadeiro/falso.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Russman » Sex Fev 01, 2013 04:02
por Russman » Sex Fev 01, 2013 04:02
Você não sabia resolver a 1° equação. Então, como em quase tudo na Matemática, você transforma(não no sentido matemático do termo) esse problema em outro que você sabe resolver! Mas veja que mesmo a 2° equação sendo obtida pela manipulação da 1° elas são equações DIFERENTES que, via razões óbvias, possuem alguma ou algumas raízes em comum.
Assim,

pode solucionar a 2° forma da equação mas não a 1°. Você deve obter as soluções da 2° e testar na equação 1° e verificar qual delas que a satisfazem.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação com raizes reais
por Thays » Ter Jan 22, 2013 12:48
- 4 Respostas
- 2199 Exibições
- Última mensagem por DanielFerreira

Ter Jan 22, 2013 20:29
Equações
-
- demonstração e determinação de raizes
por tigre matematico » Sáb Out 15, 2011 23:29
- 0 Respostas
- 927 Exibições
- Última mensagem por tigre matematico

Sáb Out 15, 2011 23:29
Polinômios
-
- (ITA) Determinar No de Raízes Reais
por Carolziiinhaaah » Sáb Jun 19, 2010 11:59
- 1 Respostas
- 1218 Exibições
- Última mensagem por Douglasm

Sáb Jun 19, 2010 21:25
Álgebra Elementar
-
- Numero de raízes reais diferentes.
por matheuszila » Dom Nov 28, 2010 14:36
- 6 Respostas
- 3298 Exibições
- Última mensagem por matheuszila

Sex Dez 10, 2010 22:30
Logaritmos
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8111 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{3x-2}=\sqrt[]{x} + 2 \sqrt[]{3x-2}=\sqrt[]{x} + 2](/latexrender/pictures/9ab84a666b2608567531a7a3bfdd70e7.png) :
:![{\left(\sqrt[]{3x-2} \right)}^{2}={\left(\sqrt[]{x}+2 \right)}^{2}\Rightarrow{x}^{2}-10x+9=0 {\left(\sqrt[]{3x-2} \right)}^{2}={\left(\sqrt[]{x}+2 \right)}^{2}\Rightarrow{x}^{2}-10x+9=0](/latexrender/pictures/c8cdbe689fd85da2ea25a208180628de.png)

![\sqrt[]{3x-2}=\sqrt[]{x} + 2 \sqrt[]{3x-2}=\sqrt[]{x} + 2](/latexrender/pictures/9ab84a666b2608567531a7a3bfdd70e7.png) :
:![{\left(\sqrt[]{3x-2} \right)}^{2}={\left(\sqrt[]{x}+2 \right)}^{2}\Rightarrow{x}^{2}-10x+9=0 {\left(\sqrt[]{3x-2} \right)}^{2}={\left(\sqrt[]{x}+2 \right)}^{2}\Rightarrow{x}^{2}-10x+9=0](/latexrender/pictures/c8cdbe689fd85da2ea25a208180628de.png)

 que encontraste na equação inicial, isto é, substituir
que encontraste na equação inicial, isto é, substituir  e
e 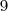 em
em 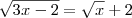 , e, verificar se é verdadeiro/falso.
, e, verificar se é verdadeiro/falso.
 pode solucionar a 2° forma da equação mas não a 1°. Você deve obter as soluções da 2° e testar na equação 1° e verificar qual delas que a satisfazem.
pode solucionar a 2° forma da equação mas não a 1°. Você deve obter as soluções da 2° e testar na equação 1° e verificar qual delas que a satisfazem.