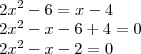Boa tarde .Primeiramente somamando-se
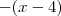
em ambos membros de

(Perceba que não vamos alterar o resultado ) vamos ter :

.
Desta forma obtermos a forma geral (ou normal ) da equação quadrática (ou do segundo grau ) .
Para responder as letras a) e b) , veja que dada equação geral grau 2

(a,b e c reais com a diferente que zero ) se

são raízes da equação

então :
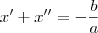
e
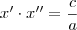
.
Tente aplicar este conceito à eq.
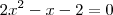
.
Uma vez que você solucionou os exercícios proposto pelas letras a) e b) na letra c) será consequência dos resultados obtidos em a) e b) .
Veja ,
Multiplicando
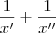
por

(Perceba que novamente não estamos alterando o resultado , pois

)
Desta forma ,
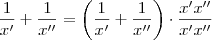
. Deixando o termo
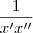
em evidência e aplicando a distributiva do termo
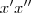
sobre a soma
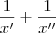
. Vamos obter ,
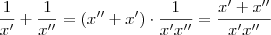
.
Tente concluir .
 +
+  =
=


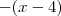 em ambos membros de
em ambos membros de  (Perceba que não vamos alterar o resultado ) vamos ter :
(Perceba que não vamos alterar o resultado ) vamos ter :  .
. (a,b e c reais com a diferente que zero ) se
(a,b e c reais com a diferente que zero ) se  são raízes da equação
são raízes da equação 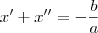 e
e 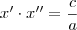 .
.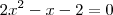 .
. 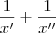 por
por  (Perceba que novamente não estamos alterando o resultado , pois
(Perceba que novamente não estamos alterando o resultado , pois  )
)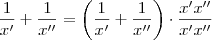 . Deixando o termo
. Deixando o termo 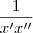 em evidência e aplicando a distributiva do termo
em evidência e aplicando a distributiva do termo 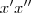 sobre a soma
sobre a soma 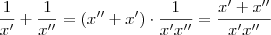 .
.
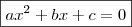

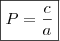
 ,
,  e
e  na equação e substituir na fórmula (soma e produto). No entanto, devemos 'arrumar' a eq. do enunciado...
na equação e substituir na fórmula (soma e produto). No entanto, devemos 'arrumar' a eq. do enunciado...