[Equação do Segundo Grau] Questão da Fuvest

por **ALPC** » Ter Jan 15, 2013 17:25

Olá, tenho uma dúvida sobre essa questão do Fuvest 2013:

Um empreiteiro contratou um serviço com um grupo de trabalhadores pelo valor de ?$ 10.800,00 a
serem igualmente divididos entre eles. Como três desistiram do trabalho, o valor contratado foi
dividido igualmente entre os demais. Assim, o empreiteiro pagou, a cada um dos trabalhadores que
realizaram o serviço, ?$ 600,00 além do combinado no acordo original.
a) Quantos trabalhadores realizaram o serviço?
b) Quanto recebeu cada um deles?

Eu até consigo iniciar, mas não consigo prosseguir com a questão:
$\frac {10800}{x} = \frac{10800}{x-3} - 600$

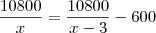
Em um vídeo eu vi que depois disso isso daria uma Equação do Segundo Grau, mas não mostrava como prosseguir depois disso. Então minha dúvida é:
Como prosseguir com a resolução desta questão?
Não estou conseguindo.

Agradeço desde ja.

por **Cleyson007** » Ter Jan 15, 2013 18:58

ALPC, seja bem-vindo(a) ao AjudaMatemática!

Vou te ajudar com a montagem das equações..

n = n° de trabalhadores que realizaram o serviço
v = valor recebido por cada um deles

R$ 10800,00 é a quantia recebida por cada um deles --> n.v = 10800 (I)

Número de trabalhadores (inicialmente) envolvolvidos no trabalho --> n + 3

Eles receberiam --> v - 600

(n + 3) (v - 600) = 10800 (II)

Agora basta resolver o sistema de equação para encontrar os valores de "n" e "v".

Abraço,

Cleyson007