d²y/dx² - 5 dy/dx + 6y = 0
RESOLUÇÃO:
equação característica:
m² - 5m + 6 = 0
resultado das raízes: m1 = 3
m2 = 2
yc = c1.
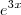+ c2.
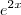
Obs.: daqui pra frente é que eu não sei se continuo com a equação particular e depois fazendo a substituição de (2) que é da yp na equação diferencial principal (1) pra daí então encontrar a solução geral que é y = yc + yp? POR FAVOR, ME AJUDEM! ESTOU CHEIA DE DÚVIDAS!
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)