Como faço para cacular esta função? ?((150-x)^2+30^2) + ?(50^2+x^2) =170?
a resposta de x=375/4
por moraes1321 » Ter Dez 04, 2012 17:43
por Russman » Ter Dez 04, 2012 19:13
![\sqrt[]{a} + \sqrt[]{b} = c](/latexrender/pictures/e0537a7ec2d97e2bc17d03d2994dc73c.png "\sqrt[]{a} + \sqrt[]{b} = c")
![(\sqrt[]{a} + \sqrt[]{b})^2 = c^2](/latexrender/pictures/96b9c3a4166d05844c99812d66aaf1ff.png "(\sqrt[]{a} + \sqrt[]{b})^2 = c^2")
![\sqrt[]{a}\sqrt[]{a} + 2\sqrt[]{a}\sqrt[]{b} + \sqrt[]{b}\sqrt[]{b} = c^2](/latexrender/pictures/1b8b571a82bc68a84964d53a427dd8dd.png "\sqrt[]{a}\sqrt[]{a} + 2\sqrt[]{a}\sqrt[]{b} + \sqrt[]{b}\sqrt[]{b} = c^2")
![a + 2\sqrt[]{ab} + b = c^2](/latexrender/pictures/7de2640a04e495cd9df58a2846326f34.png "a + 2\sqrt[]{ab} + b = c^2")
![2\sqrt[]{ab} = c^2 - a - b](/latexrender/pictures/030fe7d34cf01798ebcbbc31a5dada4f.png "2\sqrt[]{ab} = c^2 - a - b")
![(\sqrt[]{ab})^2 = (\frac{c^2-a-b}{2})^2](/latexrender/pictures/fb5c284d0b421e991d44b9ee4886c72d.png "(\sqrt[]{ab})^2 = (\frac{c^2-a-b}{2})^2")
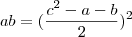
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)