 por qwepoi678 » Ter Ago 28, 2012 16:46
por qwepoi678 » Ter Ago 28, 2012 16:46
Ajuda equação de 2º grau
Olá, sou um aluno do 9° ano e recentemente o professor passou em minha prova a seguinte questão:
Papai noel gastou R$ 400,00 na compra de bolas para distribuir no dia de natal. Com um desconto de R$ 4,00 em cada uma, teria comprado 5 bolas a mais. Quantas bolas ele comprou?
Respondi em minha prova que a resposta era 20 bolas, pois 400/20 daria 20 reais cada bola, e 4 reais a menos em cada bola daria 16. 400 /16 é igual a 25, 25 - 5 é igual ao numero de bola que ele comprou.
A resposta dita pelo professor foi 16 pois segundo ele, 400/x - 4 = x + 5, e fazendo esta equação ele chegou aos resultados 16 e -25 dizendo que o resultado era 16.
Estou com dificuldade para entender a resposta dele pois 16bolas + 5 bolas daria 21 e sendo 16 bolas o preço de cada seria 25 reais, 25 - 4 reais daria 21 também, mas 21. 21 não da 400 reais.
Alguém poderia me ajudar a entender por favor?
-
qwepoi678
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Ago 28, 2012 16:37
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por qwepoi678 » Ter Ago 28, 2012 22:47
por qwepoi678 » Ter Ago 28, 2012 22:47
Mas por que p-4 = q+5?
Diz-se que se o preço fosse 4 reais mais barato daria para comprar mais 5 bolas, porém não diz que a quantidade + 5 é igual ao preço -4.
-
qwepoi678
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Ago 28, 2012 16:37
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Qua Ago 29, 2012 09:59
por MarceloFantini » Qua Ago 29, 2012 09:59
Acredito que errei nas minhas considerações anteriores, sua resposta está correta. Papai noel tem 400 reais disponíveis para comprar as bolas. Com o preço

ele comprou

bolas gastando 400 reais, logo

.
Se cada bola custasse 4 reais a menos, ou seja

, compraria 5 bolas a mais, ou seja

, porém continuaria gastando 400 reais, portanto temos
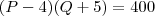
.
Expandindo temos
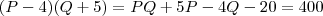
, mas a primeira equação diz que

, logo

.
Isolando

e substituindo na primeira segue

. As soluções são

, que é descartada pois a quantidade é maior que zero e inteira, e
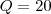
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda Equação 2º Grau
por andrelpti » Dom Out 10, 2010 18:04
- 4 Respostas
- 2389 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 00:54
Sistemas de Equações
-
- Ajuda na equação do 1 grau
por zekinha » Seg Jun 27, 2011 00:38
- 12 Respostas
- 7847 Exibições
- Última mensagem por Fabio Cabral

Ter Jun 28, 2011 00:43
Álgebra Elementar
-
- Ajuda equação de 2º grau
por MarceloFantini » Ter Ago 28, 2012 19:22
- 0 Respostas
- 967 Exibições
- Última mensagem por MarceloFantini

Ter Ago 28, 2012 19:22
Equações
-
- ajuda com equaçao de segundo grau
por jmontenegro » Dom Fev 19, 2012 12:04
- 1 Respostas
- 1577 Exibições
- Última mensagem por fraol

Dom Fev 19, 2012 22:58
Funções
-
- Equação do segundo grau, ajuda.
por LuizCarlos » Dom Mai 13, 2012 13:02
- 2 Respostas
- 1980 Exibições
- Última mensagem por LuizCarlos

Dom Mai 13, 2012 17:17
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ele comprou
ele comprou  bolas gastando 400 reais, logo
bolas gastando 400 reais, logo  .
.  , compraria 5 bolas a mais, ou seja
, compraria 5 bolas a mais, ou seja  , porém continuaria gastando 400 reais, portanto temos
, porém continuaria gastando 400 reais, portanto temos 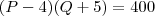 .
.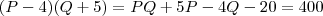 , mas a primeira equação diz que
, mas a primeira equação diz que  , logo
, logo  .
. . As soluções são
. As soluções são  , que é descartada pois a quantidade é maior que zero e inteira, e
, que é descartada pois a quantidade é maior que zero e inteira, e 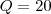 .
.
