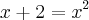por rafaelmtmtc » Sáb Abr 18, 2009 20:45
por rafaelmtmtc » Sáb Abr 18, 2009 20:45
Preciso de ajuda na questão
Escreva as implicações lógicas que correspondem a resolução da equação
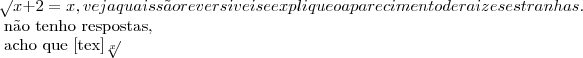
x está contido no universo de x e também que 2 está contido no universo de x, assim
![\sqrt[x]{} \sqrt[x]{}](/latexrender/pictures/33121fff2a2f571590ac334ebe677a75.png)
x+2=x é o próprio universo de x, porém não estou conseguindo fazer a expressão e muito menos o restante do exercicio,
desde já estarei grato pela atenção
-
rafaelmtmtc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 18, 2009 18:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic/bac matematica
- Andamento: cursando
 por Marcampucio » Sáb Abr 18, 2009 21:33
por Marcampucio » Sáb Abr 18, 2009 21:33
O que você escreveu está quase incompreensível...
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por rafaelmtmtc » Sáb Abr 18, 2009 23:15
por rafaelmtmtc » Sáb Abr 18, 2009 23:15
Aqui vai novamente a questão:
Escreva as implicações lógicas que correspondem a reolução da equação
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png)
x+2 = x
veja quais são reversiveis e explique o aparecimento de raizes estranhas.
Obrigado
-
rafaelmtmtc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 18, 2009 18:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic/bac matematica
- Andamento: cursando
 por Molina » Dom Abr 19, 2009 00:09
por Molina » Dom Abr 19, 2009 00:09
Boa noite, Rafael.
Vou dar uma pequena contribuição para esta questão.
Mas quero que outras pessoas do fórum complemente a sua questão levantada.
Vou considerar quando você diz
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png)
x+2 = x como sendo
![\sqrt[]{x+2}=x \sqrt[]{x+2}=x](/latexrender/pictures/40b4facc18a1281b19a2e95165e58014.png)
, ok?

Pois do jeito que você colocou ficou ambiguo.
Mas vamos lá:
![\sqrt[]{x+2}=x \sqrt[]{x+2}=x](/latexrender/pictures/40b4facc18a1281b19a2e95165e58014.png)
![(\sqrt[]{x+2})^2=x^2 (\sqrt[]{x+2})^2=x^2](/latexrender/pictures/2bc73301fb7cdb618efd2fcd488be658.png)
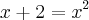

Soluções da equação do 2º grau:
+2 e
-1Agora qual a lógica que você quer disso, eu deixo para o próximo.
Fiz certo até agora?
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rafaelmtmtc » Dom Abr 19, 2009 12:47
por rafaelmtmtc » Dom Abr 19, 2009 12:47
Professor muito obrigado, isto já me ajudou a compreender o exercicio.
abraços
rafael
-
rafaelmtmtc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Abr 18, 2009 18:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic/bac matematica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conjunto vazio está dentro de outro conjunto vazio?
por JDomingos » Dom Jul 20, 2014 07:41
- 1 Respostas
- 2223 Exibições
- Última mensagem por DanielFerreira

Dom Jul 20, 2014 12:14
Conjuntos
-
- (ESTATÍSTICA ) Teoria
 por Roberta » Ter Ago 11, 2009 23:18
por Roberta » Ter Ago 11, 2009 23:18
- 4 Respostas
- 4928 Exibições
- Última mensagem por Roberta

Qui Ago 13, 2009 15:40
Estatística
-
- Teoria dos Números
por cheese » Sáb Out 24, 2009 14:08
- 1 Respostas
- 2232 Exibições
- Última mensagem por Cleyson007

Sáb Out 24, 2009 15:10
Álgebra Elementar
-
- Teoria dos Conjuntos
por tertulia » Seg Dez 27, 2010 17:47
- 3 Respostas
- 3439 Exibições
- Última mensagem por Drakangt

Seg Dez 29, 2014 14:29
Álgebra Elementar
-
- Teoria dos números!
por Abelardo » Qui Mar 10, 2011 01:44
- 0 Respostas
- 1560 Exibições
- Última mensagem por Abelardo

Qui Mar 10, 2011 01:44
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
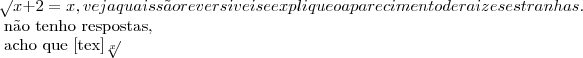 x está contido no universo de x e também que 2 está contido no universo de x, assim
x está contido no universo de x e também que 2 está contido no universo de x, assim ![\sqrt[x]{} \sqrt[x]{}](/latexrender/pictures/33121fff2a2f571590ac334ebe677a75.png) x+2=x é o próprio universo de x, porém não estou conseguindo fazer a expressão e muito menos o restante do exercicio,
x+2=x é o próprio universo de x, porém não estou conseguindo fazer a expressão e muito menos o restante do exercicio,


![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) x+2 = x
x+2 = x![\sqrt[]{x+2}=x \sqrt[]{x+2}=x](/latexrender/pictures/40b4facc18a1281b19a2e95165e58014.png) , ok?
, ok?  Pois do jeito que você colocou ficou ambiguo.
Pois do jeito que você colocou ficou ambiguo.![(\sqrt[]{x+2})^2=x^2 (\sqrt[]{x+2})^2=x^2](/latexrender/pictures/2bc73301fb7cdb618efd2fcd488be658.png)