 por Rafael16 » Seg Jan 21, 2013 20:40
por Rafael16 » Seg Jan 21, 2013 20:40
Transforme
![\sqrt[]{3-\sqrt[]{5}} \sqrt[]{3-\sqrt[]{5}}](/latexrender/pictures/99a0c7083602148917278fa706536adf.png)
numa soma de radicais simples.
A fórmula que eu aprendi para resolver isso é
![\sqrt[]{A+-\sqrt[]{B}}=\sqrt[]{\frac{A+C}{2}} +- \sqrt[]{\frac{A-C}{2}} \sqrt[]{A+-\sqrt[]{B}}=\sqrt[]{\frac{A+C}{2}} +- \sqrt[]{\frac{A-C}{2}}](/latexrender/pictures/b6a6290bfcb01f83b781b1abf18d0aa6.png)
, onde
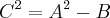
Resolvendo isso chega no resultado
![\sqrt[]{\frac{5}{2}}-\sqrt[]{\frac{1}{2}} \sqrt[]{\frac{5}{2}}-\sqrt[]{\frac{1}{2}}](/latexrender/pictures/6093a312e962eda411b796a129294818.png)
Mas a resposta não teria que ser
![\sqrt[]{\frac{5}{2}}+ -\sqrt[]{\frac{1}{2}} \sqrt[]{\frac{5}{2}}+ -\sqrt[]{\frac{1}{2}}](/latexrender/pictures/2abc6647c5404505c3ab67d0b5356ca3.png)
? Pois na fórmula temos os sinais "mais ou menos".
E acontece de ter outros exemplos de ter somente o sinal '+'.
Não estou conseguindo entender isso.
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Seg Jan 21, 2013 20:53
por Russman » Seg Jan 21, 2013 20:53
A fórmula é
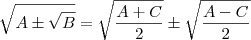
.
Ou seja, se for mais do lado esquerdo é mais do lado direito. Se for menos do lado esquerdo é menos do lado direito .
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Rafael16 » Seg Jan 21, 2013 20:53
por Rafael16 » Seg Jan 21, 2013 20:53
Valeu!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Radical duplo
por Maria Livia » Sex Fev 22, 2013 00:10
- 1 Respostas
- 14302 Exibições
- Última mensagem por DanielFerreira

Sex Fev 22, 2013 01:11
Álgebra Elementar
-
- arco duplo
por MERLAYNE » Qua Abr 04, 2012 19:52
- 1 Respostas
- 2494 Exibições
- Última mensagem por MarceloFantini

Qua Abr 04, 2012 23:57
Trigonometria
-
- [Arco Duplo]Cos(2a)
por Giudav » Sáb Set 15, 2012 12:48
- 2 Respostas
- 1924 Exibições
- Última mensagem por DanielFerreira

Sáb Set 15, 2012 22:38
Trigonometria
-
- [Integral Duplo]
por pires_ » Seg Mai 20, 2013 18:42
- 7 Respostas
- 4207 Exibições
- Última mensagem por young_jedi

Qui Mai 23, 2013 16:50
Cálculo: Limites, Derivadas e Integrais
-
- Duvida Op. Radical
por Andrewo » Seg Mar 05, 2012 11:09
- 1 Respostas
- 2050 Exibições
- Última mensagem por MarceloFantini

Seg Mar 05, 2012 13:13
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{3-\sqrt[]{5}} \sqrt[]{3-\sqrt[]{5}}](/latexrender/pictures/99a0c7083602148917278fa706536adf.png) numa soma de radicais simples.
numa soma de radicais simples.![\sqrt[]{A+-\sqrt[]{B}}=\sqrt[]{\frac{A+C}{2}} +- \sqrt[]{\frac{A-C}{2}} \sqrt[]{A+-\sqrt[]{B}}=\sqrt[]{\frac{A+C}{2}} +- \sqrt[]{\frac{A-C}{2}}](/latexrender/pictures/b6a6290bfcb01f83b781b1abf18d0aa6.png) , onde
, onde 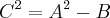
![\sqrt[]{\frac{5}{2}}-\sqrt[]{\frac{1}{2}} \sqrt[]{\frac{5}{2}}-\sqrt[]{\frac{1}{2}}](/latexrender/pictures/6093a312e962eda411b796a129294818.png)
![\sqrt[]{\frac{5}{2}}+ -\sqrt[]{\frac{1}{2}} \sqrt[]{\frac{5}{2}}+ -\sqrt[]{\frac{1}{2}}](/latexrender/pictures/2abc6647c5404505c3ab67d0b5356ca3.png) ? Pois na fórmula temos os sinais "mais ou menos".
? Pois na fórmula temos os sinais "mais ou menos".

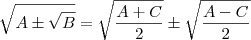 .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.