 por GehSillva7 » Qui Fev 25, 2016 12:55
por GehSillva7 » Qui Fev 25, 2016 12:55
Seja p > 0 um numero primo e seja Q[sqrt(p)] = {a+b sqrt(p); a, b E Q}. Defina as operações + e . em Q[ sqrt(p] como (a+b sqrt(p)) + (c + d sqrt(p)) = (a+c)+(b+d) sqrt(p) e (a+b sqrt(p)) . (c + d sqrt(p)) = (ac + pbd) + (ad+bc) sqrt(p). Mostre que Q[sqrt(p)] é um corpo.
-
GehSillva7
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Fev 23, 2014 21:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por adauto martins » Dom Fev 28, 2016 13:38
por adauto martins » Dom Fev 28, 2016 13:38
pelo q. pude traduzir do q. vc escreveu e mostrar q...Q={
![a+b\sqrt[]{p} a+b\sqrt[]{p}](/latexrender/pictures/99f8728343f5210cbbcb8401d4dd6adf.png)
,onde a,b,p
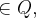
,p primo}...bom,um corpo é um espaço vetorial de dimensao nula,entao temows aquelas 8 propriedades a ser verificadas,farei algumas,tdbem...
1)
![0\in Q, pois 0+x=(0+0\sqrt[]{p})+(a+b\sqrt[]{p})=(0+a)+(0+b)\sqrt[]{p}=a+b\sqrt[]{p}=x 0\in Q, pois 0+x=(0+0\sqrt[]{p})+(a+b\sqrt[]{p})=(0+a)+(0+b)\sqrt[]{p}=a+b\sqrt[]{p}=x](/latexrender/pictures/a82f8aa2d2ad3922213cb5b75e3fc31a.png)
...
2)
![1\in Q,pois...1.x=(1+0\sqrt[]{p}).(a+b\sqrt[]{p})=(1.a+p.0)+(1.b+0.p.b)\sqrt[]{p}=a+b\sqrt[]{p}=x 1\in Q,pois...1.x=(1+0\sqrt[]{p}).(a+b\sqrt[]{p})=(1.a+p.0)+(1.b+0.p.b)\sqrt[]{p}=a+b\sqrt[]{p}=x](/latexrender/pictures/bc2a4ec8df011955d665fbe042c2c6d8.png)
...
3)seja
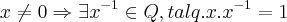
,de fato...
![x.{x}^{-1}=(a+b\sqrt[]{p}).(1/(a+b\sqrt[]{p})=(a+b\sqrt[]{p}).(a-b\sqrt[]{p})/({a}^{2}-p.{b}^{2})={a}^{2}-p.{b}^{2}/({a}^{2}-p.{b}^{2})=1 x.{x}^{-1}=(a+b\sqrt[]{p}).(1/(a+b\sqrt[]{p})=(a+b\sqrt[]{p}).(a-b\sqrt[]{p})/({a}^{2}-p.{b}^{2})={a}^{2}-p.{b}^{2}/({a}^{2}-p.{b}^{2})=1](/latexrender/pictures/a499118cc6998a170a2253c2069e29d3.png)
...as outras 5 sao mais facieis...verifique-as...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por GehSillva7 » Dom Fev 28, 2016 15:40
por GehSillva7 » Dom Fev 28, 2016 15:40
Show! Muito obrigada!
-
GehSillva7
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Fev 23, 2014 21:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![a+b\sqrt[]{p} a+b\sqrt[]{p}](/latexrender/pictures/99f8728343f5210cbbcb8401d4dd6adf.png) ,onde a,b,p
,onde a,b,p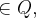 ,p primo}...bom,um corpo é um espaço vetorial de dimensao nula,entao temows aquelas 8 propriedades a ser verificadas,farei algumas,tdbem...
,p primo}...bom,um corpo é um espaço vetorial de dimensao nula,entao temows aquelas 8 propriedades a ser verificadas,farei algumas,tdbem...![0\in Q, pois 0+x=(0+0\sqrt[]{p})+(a+b\sqrt[]{p})=(0+a)+(0+b)\sqrt[]{p}=a+b\sqrt[]{p}=x 0\in Q, pois 0+x=(0+0\sqrt[]{p})+(a+b\sqrt[]{p})=(0+a)+(0+b)\sqrt[]{p}=a+b\sqrt[]{p}=x](/latexrender/pictures/a82f8aa2d2ad3922213cb5b75e3fc31a.png) ...
...![1\in Q,pois...1.x=(1+0\sqrt[]{p}).(a+b\sqrt[]{p})=(1.a+p.0)+(1.b+0.p.b)\sqrt[]{p}=a+b\sqrt[]{p}=x 1\in Q,pois...1.x=(1+0\sqrt[]{p}).(a+b\sqrt[]{p})=(1.a+p.0)+(1.b+0.p.b)\sqrt[]{p}=a+b\sqrt[]{p}=x](/latexrender/pictures/bc2a4ec8df011955d665fbe042c2c6d8.png) ...
...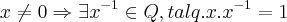 ,de fato...
,de fato...![x.{x}^{-1}=(a+b\sqrt[]{p}).(1/(a+b\sqrt[]{p})=(a+b\sqrt[]{p}).(a-b\sqrt[]{p})/({a}^{2}-p.{b}^{2})={a}^{2}-p.{b}^{2}/({a}^{2}-p.{b}^{2})=1 x.{x}^{-1}=(a+b\sqrt[]{p}).(1/(a+b\sqrt[]{p})=(a+b\sqrt[]{p}).(a-b\sqrt[]{p})/({a}^{2}-p.{b}^{2})={a}^{2}-p.{b}^{2}/({a}^{2}-p.{b}^{2})=1](/latexrender/pictures/a499118cc6998a170a2253c2069e29d3.png) ...as outras 5 sao mais facieis...verifique-as...
...as outras 5 sao mais facieis...verifique-as...



 , avisa que eu resolvo.
, avisa que eu resolvo.

