 por juliohenriquelima14 » Sáb Dez 13, 2014 23:20
por juliohenriquelima14 » Sáb Dez 13, 2014 23:20
Boa noite!
Estou praticando algumas questões que envolve as propriedades da divisibilidade, já consegui resolver algumas, porém o assunto ainda não ficou tão claro.
Desde já agradeço a todo que vêm ajudando, o fórum tem sido de extrema importância para o meu desenvolvimento no meio acadêmico.
1-Mostre que para todo n
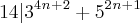
Minha ideia é a seguinte:
i) Queremos mostrar que

ii)

iii)Por fim, a proposição
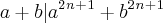
garante que
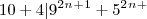
-
juliohenriquelima14
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Nov 01, 2014 09:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema da Informação
- Andamento: cursando
 por adauto martins » Dom Dez 21, 2014 11:49
por adauto martins » Dom Dez 21, 2014 11:49
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
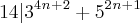


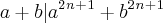 garante que
garante que 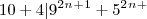


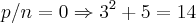
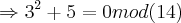
 ,ou seja
,ou seja 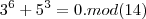
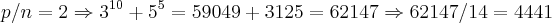 ,logo
,logo  ...observe q. os numeros calculados sao todos combinaçoes de
...observe q. os numeros calculados sao todos combinaçoes de 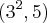 entao,se tomarmos p/n=k
entao,se tomarmos p/n=k seja multiplo de 14...
seja multiplo de 14...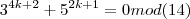
 ...de fato,p/n=k+1
...de fato,p/n=k+1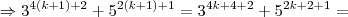
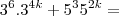
 ,logo
,logo 


 , avisa que eu resolvo.
, avisa que eu resolvo.

