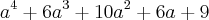 .
.Resposta:
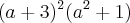

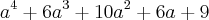 .
.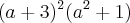


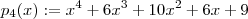 .
.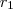 é uma raiz de
é uma raiz de 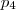 então existe um polinômio de grau 3 tal que o seu produto por
então existe um polinômio de grau 3 tal que o seu produto por 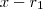 dá
dá 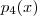 . Descobrindo-se uma raiz deste polinômio de grau 3 , o processo contínua ... obterá um polinômio de grau 2 tal que seu produto por
. Descobrindo-se uma raiz deste polinômio de grau 3 , o processo contínua ... obterá um polinômio de grau 2 tal que seu produto por 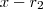 dá exatamente este polinômio de grau 3 . O método termina quando o polinômio não admitir raízes reais .
dá exatamente este polinômio de grau 3 . O método termina quando o polinômio não admitir raízes reais .  . A titulo de exemplificar ,
. A titulo de exemplificar , 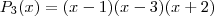 é exatamente
é exatamente 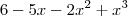 . Dividindo
. Dividindo 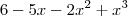 por
por  obterá
obterá 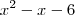 , encontrando as raízes deste polinômio tem-se ele escrito na forma fatorada
, encontrando as raízes deste polinômio tem-se ele escrito na forma fatorada  .Juntando tudo tem-se
.Juntando tudo tem-se ![]6-5 x-2 x^2+x^3 = (x-1)(x-3)(x+2) ]6-5 x-2 x^2+x^3 = (x-1)(x-3)(x+2)](/latexrender/pictures/35842430ac30ae7eb600f687b0bca0a7.png) .
. 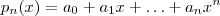 com
com 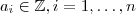 e
e 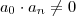 . Suponha que
. Suponha que  é uma raiz inteira deste polinômio , então
é uma raiz inteira deste polinômio , então  divide
divide 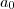 .
. 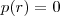 o que implica que
o que implica que 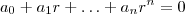
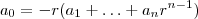 . Desde que
. Desde que 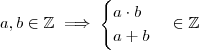 , então
, então 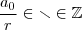
 admite uma raiz inteira .
admite uma raiz inteira .  inteiro t.q ,
inteiro t.q , 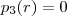 , como todos os coef. de
, como todos os coef. de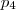 são positivos , então só pode ser
são positivos , então só pode ser 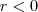 . Pergunta : Quais os divisores negativos de
. Pergunta : Quais os divisores negativos de 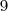 ?
? 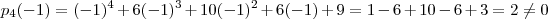
![p_4(-3) = (-3)^4 + 6(-3)^3 +10(-3)^2 +6(-3) + 3 = (-3)^2[ \underbrace{(-3)^2 + 6(-3) +10 -1}_{9-18 +10 -1 = 0 } ] = 0 p_4(-3) = (-3)^4 + 6(-3)^3 +10(-3)^2 +6(-3) + 3 = (-3)^2[ \underbrace{(-3)^2 + 6(-3) +10 -1}_{9-18 +10 -1 = 0 } ] = 0](/latexrender/pictures/3d4ade328e93dc76233fa8b80ee7cd7a.png) .
.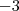 é uma raiz de
é uma raiz de 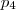 . Dividindo
. Dividindo 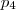 por
por 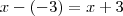 obterá
obterá 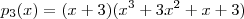 .
.  inteiro t.q
inteiro t.q  raiz de
raiz de 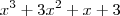 . Logo
. Logo  divide
divide  (note que r < 0 )
(note que r < 0 ) ![(-3)^3 + 3(-3)^2 + (-3) + 3 = (-3)[\underbrace{(-3)^2 + 3(-3) + 1 + -1}_{0}] = 0 (-3)^3 + 3(-3)^2 + (-3) + 3 = (-3)[\underbrace{(-3)^2 + 3(-3) + 1 + -1}_{0}] = 0](/latexrender/pictures/1ce7825030edeac1a313aeb60b74c6cc.png) . Dividindo-se
. Dividindo-se 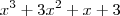 por
por 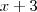 obterá
obterá 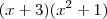 . Como
. Como 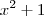 não admite raízes reais então o processo finaliza-se e tem-se a forma fatorada requerida .
não admite raízes reais então o processo finaliza-se e tem-se a forma fatorada requerida .  de grau
de grau  ,
, 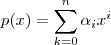 e que se sabe que
e que se sabe que  é a sua raiz . Escreveremos
é a sua raiz . Escreveremos  sob a seguinte forma
sob a seguinte forma 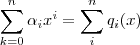 onde
onde 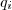 são polinômios tais que
são polinômios tais que 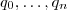 compartilham a mesma raiz real
compartilham a mesma raiz real  , i.e ,
, i.e ,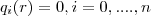 e além disso eles cumprem com
e além disso eles cumprem com 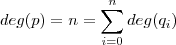 . A vantagem é que alguns dos
. A vantagem é que alguns dos 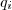 certamente possuem grau menor que n (possa ser que todos q_i possuem grau n ) o que facilita determinar outra raiz de cada polinômio .
certamente possuem grau menor que n (possa ser que todos q_i possuem grau n ) o que facilita determinar outra raiz de cada polinômio . 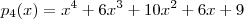 . Usando (ii) descobre-se que
. Usando (ii) descobre-se que 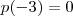 . E segue que
. E segue que 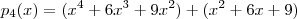 . Verifica-se que
. Verifica-se que 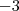 (com multiplicidade 2) é raiz de
(com multiplicidade 2) é raiz de 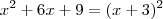 logo também o é de
logo também o é de 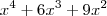 , mas !
, mas ! 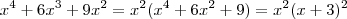 e com isso ganhamos que
e com isso ganhamos que 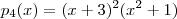 .
. 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante