 por Sobreira » Qui Ago 22, 2013 01:53
por Sobreira » Qui Ago 22, 2013 01:53
Na seguinte expressão abaixo, eu tentei igualar a x para resolver mas não consigo passar de um determinado ponto.
![\sqrt[]{9+4\sqrt[]{5}} \sqrt[]{9+4\sqrt[]{5}}](/latexrender/pictures/990067d1b6150499cd1007b4aa365ce4.png)
![\sqrt[]{9+\sqrt[]{80}} \sqrt[]{9+\sqrt[]{80}}](/latexrender/pictures/a7d952bbd60083d9842aa94fa3e2c7c2.png)
![9+\sqrt[]{80}={x}^{2} 9+\sqrt[]{80}={x}^{2}](/latexrender/pictures/e84a1ead665bed6bd5124d3df5944d1e.png)
A partir daí como posso fazer para simplificar mais ??
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Renato_RJ » Qui Ago 22, 2013 12:54
por Renato_RJ » Qui Ago 22, 2013 12:54
Bom dia !!
Note que você tem uma equação quadrática, veja:
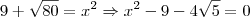
Agora é achar as raízes dessa equação:
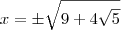
Abraços !!
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Sobreira » Qui Ago 22, 2013 18:12
por Sobreira » Qui Ago 22, 2013 18:12
Pois bem. Realizando isto que você prôpos eu acabei por retornar à equação inicial.
Eu quero simplifica-lá além do passo que eu cheguei.
Pensei em elevar novamente ao quadrado, mas aí eu teria

.
Quero terminar através de simplificação, tratando a equação como uma irracional.
Não quero calcular o valor através de uma calculadora (convenhamos que não é das tarefas mais simples encontrar raízes não exatas, como por exemplo, primeiro a raiz de 5 depois a raiz do resultado disso vezes 4 +9 na mão.)
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação de expressão
por Cleyson007 » Qui Jan 14, 2010 22:13
- 3 Respostas
- 13182 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 16, 2010 19:12
Estatística
-
- Simplificação de expressão
por maria cleide » Dom Mai 08, 2011 17:14
- 1 Respostas
- 1404 Exibições
- Última mensagem por Molina

Dom Mai 08, 2011 17:49
Polinômios
-
- Simplificação(UNIFOR)-A expressão
por wgf » Seg Mai 27, 2013 20:26
- 4 Respostas
- 9661 Exibições
- Última mensagem por DanielFerreira

Ter Mai 01, 2018 22:54
Álgebra Elementar
-
- Regras de simplificação de expressão
 por xdleoskk8 » Sáb Fev 15, 2014 12:29
por xdleoskk8 » Sáb Fev 15, 2014 12:29
- 3 Respostas
- 3632 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 15, 2014 14:17
Equações
-
- simplificação de expressão entre conjuntos
por jojo » Ter Abr 06, 2010 16:49
- 1 Respostas
- 4018 Exibições
- Última mensagem por Lucio Carvalho

Ter Abr 06, 2010 21:26
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{9+4\sqrt[]{5}} \sqrt[]{9+4\sqrt[]{5}}](/latexrender/pictures/990067d1b6150499cd1007b4aa365ce4.png)
![\sqrt[]{9+\sqrt[]{80}} \sqrt[]{9+\sqrt[]{80}}](/latexrender/pictures/a7d952bbd60083d9842aa94fa3e2c7c2.png)
![9+\sqrt[]{80}={x}^{2} 9+\sqrt[]{80}={x}^{2}](/latexrender/pictures/e84a1ead665bed6bd5124d3df5944d1e.png)

![\sqrt[]{9+4\sqrt[]{5}} \sqrt[]{9+4\sqrt[]{5}}](/latexrender/pictures/990067d1b6150499cd1007b4aa365ce4.png)
![\sqrt[]{9+\sqrt[]{80}} \sqrt[]{9+\sqrt[]{80}}](/latexrender/pictures/a7d952bbd60083d9842aa94fa3e2c7c2.png)
![9+\sqrt[]{80}={x}^{2} 9+\sqrt[]{80}={x}^{2}](/latexrender/pictures/e84a1ead665bed6bd5124d3df5944d1e.png)

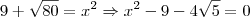
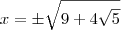

 .
.

 .
.



