[Simplificação] Dúvida em relação ao resultado

por **stilobreak** » Sáb Mar 23, 2013 02:43

Exercício: Simplifique a expressão $100^\frac{-2}{3}+(\frac{1}{27})^\frac{-4}{3}-(625)^-^0^.^7^5$

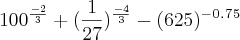
O que eu Fiz:
-----------------------------------------------------------------------------------
$\frac{1}{\sqrt[3]{100^2}}+(27)^\frac{4}{3}-(625)^\frac{-3}{4}$
-----------------------------------------------------------------------------------
$\frac{1}{\sqrt[3]{100^2}}+81-\frac{1}{\sqrt[4]{625^3}}$
-----------------------------------------------------------------------------------
$\frac{\sqrt[3]{100}}{100}+81-\frac{1}{125}$
-----------------------------------------------------------------------------------
$\frac{\sqrt[3]{100}}{100}+\frac{10124}{125}$
-----------------------------------------------------------------------------------
$\frac{5\sqrt[3]{100}+40496}{500}$

Bom cheguei até ai, e acredito que é o resultado correto, pois tenho um programa que resolve a conta automaticamente e chegou até ai também...

Porém, no gabarito a resposta é:
$\frac{40501}{500}$

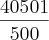
Afinal, o gabarito está errado?, ou tem como realmente tirar essa raiz cúbica de 100 daí?...

(Quero aproveitar e parabenizar o Fórum, que está me ajudando muito, pois estudo sozinho...)

por **DanielFerreira** » Sex Mar 29, 2013 02:20

Olá stilobreak,
não percebi erro algum em suas contas!

Até a próxima!

Daniel.

[Simplificação] Dúvida em relação ao resultado

[Simplificação] Dúvida em relação ao resultado

[Simplificação] Dúvida em relação ao resultado

Re: [Simplificação] Dúvida em relação ao resultado

Quem está online