 por invader_zim » Ter Fev 12, 2013 11:31
por invader_zim » Ter Fev 12, 2013 11:31
Por que as raízes são equivalentes a potências de expoentes racionais?
Preciso de uma demonstração. Não basta dizer que é. Não consigo encontrar um livro que explique isso.
-
invader_zim
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Fev 11, 2013 14:41
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DanielFerreira » Ter Fev 12, 2013 12:10
por DanielFerreira » Ter Fev 12, 2013 12:10
![\\ \sqrt[a]{b} = x \\\\ \left( \sqrt[a]{b} \right)^a = x^a \\\\ \left( \sqrt[\cancel{a}]{b} \right)^{\cancel{a}} = x^a \\\\ b = x^a \\ \sqrt[a]{b} = x \\\\ \left( \sqrt[a]{b} \right)^a = x^a \\\\ \left( \sqrt[\cancel{a}]{b} \right)^{\cancel{a}} = x^a \\\\ b = x^a](/latexrender/pictures/894618b17fba7ccaa2ce29f38f9ae9e7.png)
Eliminamos o expoente de

multiplicando-o por

, de acordo com a propriedade de potência.
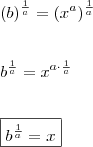
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por invader_zim » Ter Fev 12, 2013 12:15
por invader_zim » Ter Fev 12, 2013 12:15
Ótima demonstração, danjr5. Obrigado!
Saberia me dizer onde posso encontrar livros com demonstrações desse tipo?
-
invader_zim
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Fev 11, 2013 14:41
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DanielFerreira » Ter Fev 12, 2013 12:24
por DanielFerreira » Ter Fev 12, 2013 12:24
Invander_zim,
infelizmente não sei. Mas, vale ressaltar que usei as propriedades de potência; você já domina esse assunto?
Até a próxima!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potencias com expoentes diferentes - Subtrair?
por Soprano » Dom Fev 14, 2016 10:25
- 7 Respostas
- 7573 Exibições
- Última mensagem por Soprano

Dom Fev 14, 2016 17:05
Números Complexos
-
- Teorema Raizes Racionais
por joaofonseca » Sáb Abr 30, 2011 13:01
- 2 Respostas
- 2377 Exibições
- Última mensagem por joaofonseca

Sáb Abr 30, 2011 13:48
Funções
-
- Dúvida em equação com potências de 10
por Larry Crowne » Seg Mai 21, 2012 16:57
- 2 Respostas
- 1815 Exibições
- Última mensagem por Larry Crowne

Ter Mai 22, 2012 13:10
Álgebra Elementar
-
- Dúvida no cálculo de Potências
por zenildo » Qui Mai 05, 2016 11:33
- 0 Respostas
- 768 Exibições
- Última mensagem por zenildo

Qui Mai 05, 2016 11:33
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida - Raízes
por hugo82 » Ter Mai 31, 2011 19:29
- 1 Respostas
- 1065 Exibições
- Última mensagem por Molina

Ter Mai 31, 2011 19:44
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\\ \sqrt[a]{b} = x \\\\ \left( \sqrt[a]{b} \right)^a = x^a \\\\ \left( \sqrt[\cancel{a}]{b} \right)^{\cancel{a}} = x^a \\\\ b = x^a \\ \sqrt[a]{b} = x \\\\ \left( \sqrt[a]{b} \right)^a = x^a \\\\ \left( \sqrt[\cancel{a}]{b} \right)^{\cancel{a}} = x^a \\\\ b = x^a](/latexrender/pictures/894618b17fba7ccaa2ce29f38f9ae9e7.png)
 multiplicando-o por
multiplicando-o por  , de acordo com a propriedade de potência.
, de acordo com a propriedade de potência.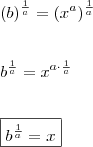




 .
.
 :
: