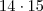Eu sou da área de humanas, então tenho muita dificuldade em questões de matemática. Se puderem me ajudar a responder a questão abaixo, agradeço. Pelo menos explicar como vou excluindo as alternativas, pois eu não sei por onde começar. Obrigado!
(UFES 2013) 12ª QUESTÃO - Sejam x e y números reais positivos. Pode-se garantir que:
A) Não existem x e y irracionais tais que x^2 ? y é racional.
B) Existem x inteiro e y racional tal que x ? y é irracional.
C) Para todo x racional e para todo y irracional, tem-se que x ? y^2 é racional.
D) Se x e y são inteiros e x ? y é divisível por um número inteiro z, então x é divisível por z ou y é divisível
por z.
E) Para todo x racional e para todo y irracional, tem-se que x^2 +
![\sqrt[]{y} \sqrt[]{y}](/latexrender/pictures/2c7054a0a5416b35c805d1e6e3dc1a54.png) é irracional.
é irracional.

 (e.g.
(e.g.  ) .Ora ,
) .Ora ,  e
e 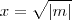 são irracionais tais que
são irracionais tais que 
 é fechado com respeito a soma e multiplicação ( i.e.
é fechado com respeito a soma e multiplicação ( i.e. 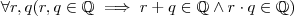 e que todo número inteiro é racional .
e que todo número inteiro é racional .![x = 0 , y = \sqrt[4]{2} x = 0 , y = \sqrt[4]{2}](/latexrender/pictures/c891f312d1dbe1deb2365b8ef65ac5f6.png)