 por Gustavo Gomes » Seg Dez 17, 2012 22:44
por Gustavo Gomes » Seg Dez 17, 2012 22:44
Olá, pessoal.
Qual o número total de divisores positivos de 10! ?
A resposta é 270.
Pensei na decomposição em fatores primos:
10! =
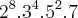
, mas daí não consegui enumerar os divisores.....
Grato.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por timoteo » Ter Dez 18, 2012 00:37
por timoteo » Ter Dez 18, 2012 00:37
boa noite.
some a cada expoente o numero 1 e depois multiplique todos os expoentes. assim:
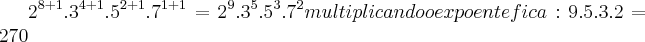
.
isso ocorre pois em cada conjunto de divisores temos os múltiplos de cada primo e é claro o numero um em cada um desses conjuntos. por isso soma-se o um a cada expoente!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Gustavo Gomes » Ter Dez 18, 2012 21:32
por Gustavo Gomes » Ter Dez 18, 2012 21:32
Agora consegui entender. Obrigado.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números positivos
por plugpc » Qua Mai 20, 2009 19:31
- 3 Respostas
- 2308 Exibições
- Última mensagem por Molina

Qua Mai 20, 2009 22:39
Álgebra Elementar
-
- Divisão de inteiros positivos
por DanielFerreira » Dom Set 16, 2012 20:59
- 2 Respostas
- 5991 Exibições
- Última mensagem por DanielFerreira

Dom Set 16, 2012 21:12
Desafios Médios
-
- Teorema inteiros positivos
por Jovani Souza » Sex Jun 07, 2013 18:05
- 0 Respostas
- 1226 Exibições
- Última mensagem por Jovani Souza

Sex Jun 07, 2013 18:05
Sequências
-
- Se os números reais positivos x e y forem tais que:
 por andersontricordiano » Seg Abr 11, 2011 15:25
por andersontricordiano » Seg Abr 11, 2011 15:25
- 7 Respostas
- 5697 Exibições
- Última mensagem por FilipeCaceres

Ter Abr 12, 2011 12:31
Logaritmos
-
- Quantidade de raizes
por estudandoMat » Seg Abr 05, 2010 00:35
- 2 Respostas
- 8713 Exibições
- Última mensagem por estudandoMat

Seg Abr 05, 2010 14:17
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
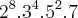 , mas daí não consegui enumerar os divisores.....
, mas daí não consegui enumerar os divisores.....
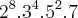 , mas daí não consegui enumerar os divisores.....
, mas daí não consegui enumerar os divisores.....
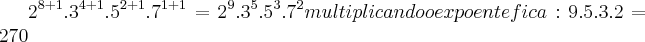 .
. 

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
