 por carlosecc » Sáb Dez 08, 2012 21:53
por carlosecc » Sáb Dez 08, 2012 21:53
Prezados me deparei com esta questão
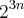
- 1 é divisivel por 7. Bem sabemos que na indução temos que realizar a base onde substituimos o n por 1 que é o P(1) apos fazemos a hipotese o P(K) onde substituimos o n por K e finalmente a conclusão onde subtituimos o n por K + 1 que é o P(K+1). Comecei a fazer assim fiz a base que da 7 = 7 ok, mas minha duvida como é que faço o P(K) e o P(K+1), se puderem me ajudar o quanto antes é que tenho prova semana que vem, desde ja gradeço a quem responder.
-
carlosecc
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 19, 2012 21:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informatica
- Andamento: cursando
 por e8group » Dom Dez 09, 2012 10:09
por e8group » Dom Dez 09, 2012 10:09
A idéia da indução é supor se algo é verdadeiro para um caso inicial ,o mesmo será verídico para o seu sucessor. Para isto devemos mostrar .
Quanto ao exercício , o resultado é claramente verdadeiro para

.
Vamos supor que este resultado é verdadeiro para

, vamos mostrar para

.
![2^{3(n+1)} - 1 = 2^{3n +3} - 1 = 2^3(2^{3n} ) - 1 = 8(2^{3n}) - 1 = 8(2^3{3n}) + (7 -8) = 8[2^{3n} -1 ] + 7 2^{3(n+1)} - 1 = 2^{3n +3} - 1 = 2^3(2^{3n} ) - 1 = 8(2^{3n}) - 1 = 8(2^3{3n}) + (7 -8) = 8[2^{3n} -1 ] + 7](/latexrender/pictures/c63704c8b3a890f752499b35fa097467.png)
.
Note que o segundo termo da soma é divisível por

.Já o primeiro , como estamos supondo que o resultado é verdadeiro para

, temos que
![8[2^{3n} -1 ] 8[2^{3n} -1 ]](/latexrender/pictures/e97aa8ecc758d911deaeb631a72d732c.png)
é divisível por

,logo concluímos que o resultado é verdadeiro para

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Dom Dez 09, 2012 10:12
por young_jedi » Dom Dez 09, 2012 10:12
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por carlosecc » Dom Dez 09, 2012 20:39
por carlosecc » Dom Dez 09, 2012 20:39
Obrigado pessoal entendi legal agora, tinha olhado antes outros topicos relacionados, mas a explicação de voces ficou blz vou aplicar no restante dos exercicios.
-
carlosecc
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 19, 2012 21:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informatica
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Provar por indução
por Cleyson007 » Sex Abr 13, 2012 15:27
- 3 Respostas
- 2130 Exibições
- Última mensagem por Cleyson007

Sex Abr 13, 2012 16:17
Álgebra Elementar
-
- Provar igualdade sem recorrer à Indução Matemática
 por EREGON » Ter Abr 14, 2015 06:29
por EREGON » Ter Abr 14, 2015 06:29
- 2 Respostas
- 4067 Exibições
- Última mensagem por e8group

Sex Abr 17, 2015 23:12
Binômio de Newton
-
- [Somatório] Provar pelo Método de Indução Matemática
por Prof Prevaricador » Dom Abr 14, 2013 16:25
- 2 Respostas
- 5066 Exibições
- Última mensagem por Prof Prevaricador

Dom Abr 14, 2013 18:35
Sequências
-
- Dúvida - Indução Finita
por Cleyson007 » Seg Mai 07, 2012 15:10
- 3 Respostas
- 1305 Exibições
- Última mensagem por MarceloFantini

Qua Mai 09, 2012 21:26
Álgebra Elementar
-
- Dúvida em Indução Matemática
por Luiz Junior » Seg Jun 18, 2012 19:45
- 2 Respostas
- 2639 Exibições
- Última mensagem por Luiz Junior

Ter Jun 19, 2012 12:49
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
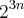 - 1 é divisivel por 7. Bem sabemos que na indução temos que realizar a base onde substituimos o n por 1 que é o P(1) apos fazemos a hipotese o P(K) onde substituimos o n por K e finalmente a conclusão onde subtituimos o n por K + 1 que é o P(K+1). Comecei a fazer assim fiz a base que da 7 = 7 ok, mas minha duvida como é que faço o P(K) e o P(K+1), se puderem me ajudar o quanto antes é que tenho prova semana que vem, desde ja gradeço a quem responder.
- 1 é divisivel por 7. Bem sabemos que na indução temos que realizar a base onde substituimos o n por 1 que é o P(1) apos fazemos a hipotese o P(K) onde substituimos o n por K e finalmente a conclusão onde subtituimos o n por K + 1 que é o P(K+1). Comecei a fazer assim fiz a base que da 7 = 7 ok, mas minha duvida como é que faço o P(K) e o P(K+1), se puderem me ajudar o quanto antes é que tenho prova semana que vem, desde ja gradeço a quem responder.

 .
.  , vamos mostrar para
, vamos mostrar para  .
. ![2^{3(n+1)} - 1 = 2^{3n +3} - 1 = 2^3(2^{3n} ) - 1 = 8(2^{3n}) - 1 = 8(2^3{3n}) + (7 -8) = 8[2^{3n} -1 ] + 7 2^{3(n+1)} - 1 = 2^{3n +3} - 1 = 2^3(2^{3n} ) - 1 = 8(2^{3n}) - 1 = 8(2^3{3n}) + (7 -8) = 8[2^{3n} -1 ] + 7](/latexrender/pictures/c63704c8b3a890f752499b35fa097467.png) .
.  .Já o primeiro , como estamos supondo que o resultado é verdadeiro para
.Já o primeiro , como estamos supondo que o resultado é verdadeiro para ![8[2^{3n} -1 ] 8[2^{3n} -1 ]](/latexrender/pictures/e97aa8ecc758d911deaeb631a72d732c.png) é divisível por
é divisível por 
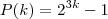
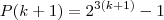



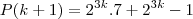
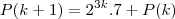
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
