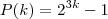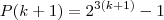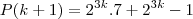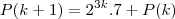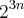Duvida em provar por Indução

por **carlosecc** » Sáb Dez 08, 2012 21:53

Prezados me deparei com esta questão ${2}^{3n}$ - 1 é divisivel por 7. Bem sabemos que na indução temos que realizar a base onde substituimos o n por 1 que é o P(1) apos fazemos a hipotese o P(K) onde substituimos o n por K e finalmente a conclusão onde subtituimos o n por K + 1 que é o P(K+1). Comecei a fazer assim fiz a base que da 7 = 7 ok, mas minha duvida como é que faço o P(K) e o P(K+1), se puderem me ajudar o quanto antes é que tenho prova semana que vem, desde ja gradeço a quem responder.

por **e8group** » Dom Dez 09, 2012 10:09

A idéia da indução é supor se algo é verdadeiro para um caso inicial ,o mesmo será verídico para o seu sucessor. Para isto devemos mostrar .

Quanto ao exercício , o resultado é claramente verdadeiro para n = 1

.

Vamos supor que este resultado é verdadeiro para

, vamos mostrar para n+1

.

$2^{3(n+1)} - 1 = 2^{3n +3} - 1 = 2^3(2^{3n} ) - 1 = 8(2^{3n}) - 1 = 8(2^3{3n}) + (7 -8) = 8[2^{3n} -1 ] + 7$ .

Note que o segundo termo da soma é divisível por

.Já o primeiro , como estamos supondo que o resultado é verdadeiro para

, temos que $8[2^{3n} -1 ]$ é divisível por

,logo concluímos que o resultado é verdadeiro para n+1

.

por **young_jedi** » Dom Dez 09, 2012 10:12

$P(k)=2^{3k}-1$

$P(k+1)=2^{3(k+1)}-1$

$P(k+1)=2^{3k+3}-1$

$P(k+1)=2^{3k}.2^3-1$

$P(k+1)=2^{3k}.8-1$

$P(k+1)=2^{3k}.7+2^{3k}-1$

$P(k+1)=2^{3k}.7+P(k)$

portanto se P(k) for divisivel por 7 então P(k+1) tambem sera
como voce ja demonstrou que P(1) é divisivel por 7 então para todo k inteiro P(k) é divisivel por 7

por **carlosecc** » Dom Dez 09, 2012 20:39

Obrigado pessoal entendi legal agora, tinha olhado antes outros topicos relacionados, mas a explicação de voces ficou blz vou aplicar no restante dos exercicios.