Bom dia, gostaria de saber se consigo entrar com recurso nesta questão pois marquei C e no gabarito esta como A.
08 - Em um torneio de futebol amador, a cada rodada duas equipes se enfrentam. A equipe vitoriosa recebe 5 pontos e a perdedora não pontua; em caso de empate, cada uma das equipes recebe 3 pontos. Todos os pontos obtidos por uma equipe são somados, e aquele que tiver a maior pontuação no final do campeonato é declarado campeão. Sabendo que ao final do torneio a equipe dos Matemáticos obteve exatamente 37 pontos, considere as seguintes afirmativas: 1. A equipe dos Matemáticos jogou pelo menos 9 partidas nesse torneio. 2. A equipe dos Matemáticos obteve no máximo 6 empates. 3. A equipe dos Matemáticos foi derrotada pelo menos uma vez nesse torneio. Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente as afirmativas 1 e 2 são verdadeiras.
c) Somente as afirmativas 1 e 3 são verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras
Obrigado


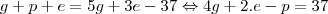
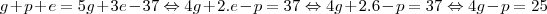



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.