Estou encarando o Introduction to Logic, do Patrick Suppes (pdf: http://tinyurl.com/oyytpee).
E na página 113 do livro (131 do pdf), 5ª questão, se pede o seguinte:
Com base nos três seguintes axiomas, prove o teorema
 :
:Axioma 1:
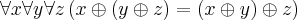
Axioma 2:
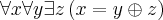
Axioma 3:

Isto é, dada Associatividade (axioma 1) e os outros 2 axiomas, demonstrar a existência do "elemento identidade à direita". Se não estou cometendo algum erro muito estúpido, esse exercício parece dificílimo. Já passei umas dez horas tentando de tudo: substituições de iguais por iguais; fazer os axiomas 2 e 3 se tornarem
 e
e 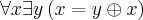 , respectivamente; prova por absurdo. Não parece haver maneira de sair dos
, respectivamente; prova por absurdo. Não parece haver maneira de sair dos  para um existencial puro
para um existencial puro 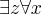 , que é o que se pede. Infelizmente não dá pra detalhar aqui a tentativa de derivação. O núcleo é:
, que é o que se pede. Infelizmente não dá pra detalhar aqui a tentativa de derivação. O núcleo é:
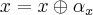
E pelo Axioma 3:
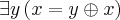
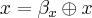
Nesse ponto não posso quantificar
 nem existencialmente, nem universalmente. O subscrito em
nem existencialmente, nem universalmente. O subscrito em 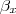 (onde
(onde 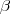 é um nome ambíguo derivado de
é um nome ambíguo derivado de 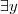 , e o subscrito indica a dependência de
, e o subscrito indica a dependência de  , que ocorria livre na fórmula original -- além disso,
, que ocorria livre na fórmula original -- além disso, 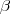 precisa ser diferente de
precisa ser diferente de 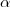 , que ocorre antes; regras de
, que ocorre antes; regras de 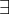 em Suppes, rs) me impede de simplesmente
em Suppes, rs) me impede de simplesmente  -quantificar sobre
-quantificar sobre  e chegar no resultado procurado
e chegar no resultado procurado 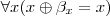 , e daí para
, e daí para  . Tampouco parece ajudar qualquer coisa a partir daqui:
. Tampouco parece ajudar qualquer coisa a partir daqui:
E daí brincando com o axioma 1. Não consigo provar que
 , e talvez isso ajudaria.
, e talvez isso ajudaria.Talvez inserir
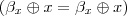 no meio e fazer alguma coisa ajude. Mas não sei o quê... Preciso de uma fórmula
no meio e fazer alguma coisa ajude. Mas não sei o quê... Preciso de uma fórmula 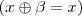 , sem subscrito, mas os axiomas parecem incapazes de produzi-la. Estou especialmente frustrado, porque esse parece ser um passo chave para usar todo o poder dos axiomas. Sigo pensando...
, sem subscrito, mas os axiomas parecem incapazes de produzi-la. Estou especialmente frustrado, porque esse parece ser um passo chave para usar todo o poder dos axiomas. Sigo pensando...

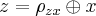
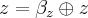
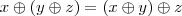


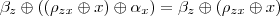
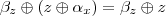

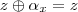
 da fórmula. E feito!
da fórmula. E feito!
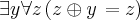 Q. E. D.
Q. E. D. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.