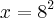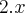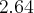por virginia » Sáb Abr 27, 2013 11:52
por virginia » Sáb Abr 27, 2013 11:52
Não consegui resolver:
Um grupo de abelhas, cujo número era igual a raiz quadrada da metade de todo enxame, posou sobre uma rosa, tendo deixado para trás 8/9 do enxame; apenas uma abelha voava ao redor de um jasmim, atraída pelo zumbido de uma de suas amigas que caíra imprudentemente na armadilha da florzinha de doce fragrância. Quantas abelhas formavam o enxame?
Tentei montar assim
![\sqrt[2]{\frac{X}{2}} \sqrt[2]{\frac{X}{2}}](/latexrender/pictures/535f9f8b8bc9f04ca45d8141f5839024.png)
SENDO QUE NÃO CHEGUEI A CONCLUSÃO NENHUMA.
Verifiquei que ele fala que ficou 8/9 do enxame logo restou 1/9 do enxame que equivale a uma abelha, seria isso?
Bom se 1/9 equivale a uma abelha que igual a 9 bom parei aqui se alguém puder me ajudar.
Att,
Virginia
-
virginia
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 12, 2012 15:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por Jhennyfer » Sáb Abr 27, 2013 17:22
por Jhennyfer » Sáb Abr 27, 2013 17:22
Oi virginia, tudo bem?
Bom, não sei muita coisa, posso estar errada, maaas...
vou tentar ajudar!
Bom, na sua resolução você colocou como grupo inteiro x e metade do grupo x/2. Certo?!
Penso assim, podemos dobrar pra facilitar...
assim podemos ter, 2x como grupo inteiro e x como metade. Concorda?
Se eu entendi bem, no enunciado diz que:
de um grupo abelhas é igual a raiz quadrada da metade de 2x... então:
![\sqrt[2]{x} \sqrt[2]{x}](/latexrender/pictures/2b552177173f128f54e48de06c7de3d9.png)
E que, esse grupo, deixou 8/9 abelhas para trás, e mais outra abelha que ficou em volta de um jasmim. Certo?
Então temos:
![\sqrt[2]{x}- \frac{8}{9}-1 \sqrt[2]{x}- \frac{8}{9}-1](/latexrender/pictures/3251313965b05957c25f54207956f0b1.png)
separamos o x...
![\sqrt[2]{x}= \frac{8}{9}+1 \sqrt[2]{x}= \frac{8}{9}+1](/latexrender/pictures/257b32bc534f003eb73bea629236d123.png)
![\sqrt[2]{x}= 8 \sqrt[2]{x}= 8](/latexrender/pictures/14adb2411d28fde32850fac69ca638e7.png)
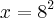

Bom, o grupo é 2x.
Substituindo...

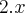
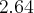

Posso estar errada, mas foi a melhor maneira que achei para resolver. Um abraço!
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problema basico de fisica usando derivadas
 por iksin » Ter Set 11, 2018 16:29
por iksin » Ter Set 11, 2018 16:29
- 1 Respostas
- 7400 Exibições
- Última mensagem por Gebe

Ter Set 11, 2018 17:38
Cálculo: Limites, Derivadas e Integrais
-
- Problema - Lógica
por RJ1572 » Seg Mar 01, 2010 13:08
- 1 Respostas
- 1572 Exibições
- Última mensagem por DanielFerreira

Qua Mar 03, 2010 08:28
Álgebra Elementar
-
- Problema Lógica
por RJ1572 » Dom Abr 04, 2010 13:22
- 1 Respostas
- 1500 Exibições
- Última mensagem por estudandoMat

Dom Abr 04, 2010 17:26
Álgebra Elementar
-
- Problema lógica
por RJ1572 » Dom Abr 04, 2010 21:32
- 1 Respostas
- 1462 Exibições
- Última mensagem por estudandoMat

Seg Abr 05, 2010 00:05
Álgebra Elementar
-
- problema de lógica
por Gladimir » Ter Fev 04, 2014 17:18
- 1 Respostas
- 1377 Exibições
- Última mensagem por fff

Ter Fev 04, 2014 17:40
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{\frac{X}{2}} \sqrt[2]{\frac{X}{2}}](/latexrender/pictures/535f9f8b8bc9f04ca45d8141f5839024.png) SENDO QUE NÃO CHEGUEI A CONCLUSÃO NENHUMA.
SENDO QUE NÃO CHEGUEI A CONCLUSÃO NENHUMA.

![\sqrt[2]{x} \sqrt[2]{x}](/latexrender/pictures/2b552177173f128f54e48de06c7de3d9.png)
![\sqrt[2]{x}- \frac{8}{9}-1 \sqrt[2]{x}- \frac{8}{9}-1](/latexrender/pictures/3251313965b05957c25f54207956f0b1.png)
![\sqrt[2]{x}= \frac{8}{9}+1 \sqrt[2]{x}= \frac{8}{9}+1](/latexrender/pictures/257b32bc534f003eb73bea629236d123.png)
![\sqrt[2]{x}= 8 \sqrt[2]{x}= 8](/latexrender/pictures/14adb2411d28fde32850fac69ca638e7.png)