 por +danile10 » Dom Fev 03, 2013 19:39
por +danile10 » Dom Fev 03, 2013 19:39
Mostre, utilizando propriedades básicas, que:
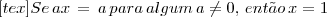
[/tex]
Eu tenho a resposta deste exercício, mas gostaria que me ajudassem a melhor compreendê-la:
Resposta: Por hipótese ax = a e como
![[tex]a\neq0\, existe\, {a}^{-1} [tex]a\neq0\, existe\, {a}^{-1}](/latexrender/pictures/05c7ab4f181a5899e9c414da307aa9b4.png)
![Logo[tex]\, {a}^{-1}(ax) = x\, Logo[tex]\, {a}^{-1}(ax) = x\,](/latexrender/pictures/8094995f56eb71fd86f4c4dbf35667e9.png)
por um lado[/tex]
e por outro
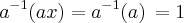
por outro.
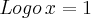
\,Não saberia reproduzir a resolução se me deparasse com este exercício
no futuro... Eu sei que é usada a propriedade de dado um número
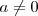
,este número possui inverso
![[tex] \,{a}^{-1} \,tal\, que \,a . {a}^{-1} = 1\, [tex] \,{a}^{-1} \,tal\, que \,a . {a}^{-1} = 1\,](/latexrender/pictures/cf722ec9b201ea0155c37f2d2ac9e191.png)
[/tex]
Mas este começo
![[tex]\, {a}^{-1} (ax)= x\, [tex]\, {a}^{-1} (ax)= x\,](/latexrender/pictures/13a20abc628fe202b2576882e055de6d.png)
[/tex] me parece confuso...
-
+danile10
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Fev 03, 2013 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Curso de Bases Matemáticas
- Andamento: cursando
 por e8group » Dom Fev 03, 2013 20:02
por e8group » Dom Fev 03, 2013 20:02
Não conseguir visualizar a resposta .
Propriedade : Existência de inverso
Para todo real b

,existe um único real

tal que
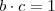
.Tal

denomina-se oposto de

,
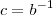
.
Portanto ,
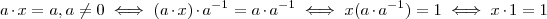
ou seja

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Fev 03, 2013 20:18
por e8group » Dom Fev 03, 2013 20:18
Você não compreendeu
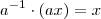
?
Veja que :

(Existência de elemento neutro )
Mas ,
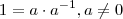
(Existência de inverso )
Disso concluímos que

(Associativa )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por +danile10 » Dom Fev 03, 2013 21:14
por +danile10 » Dom Fev 03, 2013 21:14
Não entendi ainda como isso me ajuda a provar que Se ax = a, x = 1...
Não entendi ainda menos aquela por outro lado...
Na minha cabeça vejo assim:
Assumindo x=1, pela propriedade do inverso
a . a^-1 = 1, então x = a . a^-1
Logo ax = a é o mesmo que:
a (a.a^-1) = a
Não entendo como a conclusão com a associativa vai ajudar a resolver o exercício..., mas também não acho que o que eu esteja pensando
vá me ajudar a resolvê-lo...
-
+danile10
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Fev 03, 2013 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Curso de Bases Matemáticas
- Andamento: cursando
 por e8group » Seg Fev 04, 2013 20:50
por e8group » Seg Fev 04, 2013 20:50
Boa noite . Não pode assumir que x = 1 ,pois é extamente isto que deve demonstrar .
Antes de mostrarmos ,vamos ver alguns exemplos .
Qual o valor que x deve assumir ?
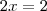
???
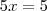
???
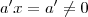
???
Parece razoável dizer que x é igual a 1 em todos os casos acima ,não é verdade ? Mas, como mostrar ?
Vamos tentar desenvolver 2x = 2 .
Temos :

.
Ora ,mas
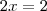
então
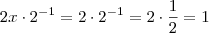
.
OBS.:Usamos todas as propriedades citadas no tópico acima .
Agora tente demonstrar que
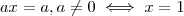
.
Comente qualquer dúvida .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números Reais - Simplificar números reais
por ZANGARO » Ter Nov 15, 2011 18:46
- 0 Respostas
- 1943 Exibições
- Última mensagem por ZANGARO

Ter Nov 15, 2011 18:46
Álgebra Elementar
-
- Números reais
por citadp » Dom Jun 24, 2012 16:02
- 1 Respostas
- 1759 Exibições
- Última mensagem por e8group

Dom Jun 24, 2012 19:22
Cálculo: Limites, Derivadas e Integrais
-
- Numeros reais
por vihalmeida » Qui Nov 15, 2012 15:19
- 1 Respostas
- 2194 Exibições
- Última mensagem por DanielFerreira

Qui Nov 15, 2012 18:40
Álgebra Elementar
-
- Estimativa de numeros reais
 por Roni Martins » Qui Fev 25, 2010 15:51
por Roni Martins » Qui Fev 25, 2010 15:51
- 1 Respostas
- 2333 Exibições
- Última mensagem por Molina

Qui Fev 25, 2010 18:30
Álgebra Elementar
-
- conjunto dos números reais
por jose henrique » Sex Set 03, 2010 21:58
- 1 Respostas
- 2127 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 [/tex]
[/tex]![[tex]a\neq0\, existe\, {a}^{-1} [tex]a\neq0\, existe\, {a}^{-1}](/latexrender/pictures/05c7ab4f181a5899e9c414da307aa9b4.png)
![Logo[tex]\, {a}^{-1}(ax) = x\, Logo[tex]\, {a}^{-1}(ax) = x\,](/latexrender/pictures/8094995f56eb71fd86f4c4dbf35667e9.png) por um lado[/tex]
por um lado[/tex]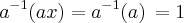 por outro.
por outro.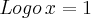
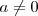 ,este número possui inverso
,este número possui inverso![[tex] \,{a}^{-1} \,tal\, que \,a . {a}^{-1} = 1\, [tex] \,{a}^{-1} \,tal\, que \,a . {a}^{-1} = 1\,](/latexrender/pictures/cf722ec9b201ea0155c37f2d2ac9e191.png) [/tex]
[/tex]![[tex]\, {a}^{-1} (ax)= x\, [tex]\, {a}^{-1} (ax)= x\,](/latexrender/pictures/13a20abc628fe202b2576882e055de6d.png) [/tex] me parece confuso...
[/tex] me parece confuso...

 ,existe um único real
,existe um único real  tal que
tal que 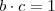 .Tal
.Tal  ,
, 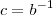 .
. 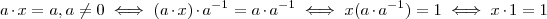 ou seja
ou seja  .
.
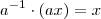 ?
?  (Existência de elemento neutro )
(Existência de elemento neutro ) 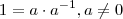 (Existência de inverso )
(Existência de inverso )  (Associativa )
(Associativa )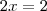 ???
???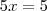 ???
???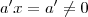 ???
??? .
. 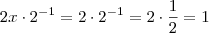 .
.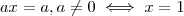 .
.