 por nietzsche » Sex Jan 06, 2012 19:48
por nietzsche » Sex Jan 06, 2012 19:48
Alguém poderia me ajudar com o seguinte problema?
Sejam
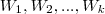
subespaços de um espaço vetorial

.
Mostre que

onde

é o subespaço gerado pela união finita dos subespaços
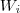
e

{

}.
Agradeço desde já.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Jan 09, 2012 19:07
por LuizAquino » Seg Jan 09, 2012 19:07
nietzsche escreveu:Sejam

,
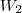
, ...,
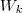
subespaços de um espaço vetorial
V.
Mostre que

onde

é o subespaço gerado pela união finita dos subespaços
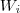
e

.
Lembre-se que para provar que

, devemos provar que para todo

, temos que

.
Seja
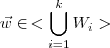
.
Como
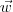
pertence a união de todos os

(com
i=1, 2, ...,
k), então ele pertence a pelo menos um desses conjuntos.
Suponha, sem perda de generalidade, que esse conjunto seja o
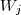
, sendo

. Ou seja, suponha que temos

.
Como

, temos que

, já que podemos escrever:

, lembrando que

com
i=1, 2, ...,
j-1,
j+1, ...,
k.
Como o
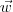
escolhido foi qualquer, podemos concluir que:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Ter Jan 10, 2012 17:16
por nietzsche » Ter Jan 10, 2012 17:16
Muito obrigado. Valeu, Luiz!
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra Linear] Ache a dimensão do subespaço...
por gabriel17carmo » Sex Jun 08, 2012 23:16
- 5 Respostas
- 3886 Exibições
- Última mensagem por gabriel17carmo

Seg Jun 11, 2012 02:42
Álgebra Linear
-
- [Álgebra Linear][Dúvida][Provar subespaço]
por Nicolas1Lane » Sex Set 12, 2014 16:45
- 1 Respostas
- 2107 Exibições
- Última mensagem por adauto martins

Qui Out 23, 2014 15:11
Álgebra Linear
-
- subespaço gerado
por Cicero ferreira » Sex Mar 14, 2014 18:23
- 1 Respostas
- 1559 Exibições
- Última mensagem por Russman

Sex Mar 14, 2014 23:00
Introdução à Álgebra Linear
-
- Subespaço gerado
por drleonunes » Qui Abr 16, 2015 21:10
- 0 Respostas
- 1523 Exibições
- Última mensagem por drleonunes

Qui Abr 16, 2015 21:10
Álgebra Linear
-
- Vetores LI e LD - Subespaço Gerado
por Cicero ferreira » Sex Mar 14, 2014 18:13
- 0 Respostas
- 2049 Exibições
- Última mensagem por Cicero ferreira

Sex Mar 14, 2014 18:13
Álgebra I para Licenciatura
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
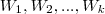 subespaços de um espaço vetorial
subespaços de um espaço vetorial  .
.
 é o subespaço gerado pela união finita dos subespaços
é o subespaço gerado pela união finita dos subespaços 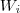
 {
{  }.
}.
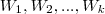 subespaços de um espaço vetorial
subespaços de um espaço vetorial  .
.
 é o subespaço gerado pela união finita dos subespaços
é o subespaço gerado pela união finita dos subespaços 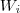
 {
{  }.
}.
,
, ...,
subespaços de um espaço vetorial V.
é o subespaço gerado pela união finita dos subespaços
.
 , devemos provar que para todo
, devemos provar que para todo  , temos que
, temos que  .
.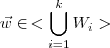 .
.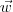 pertence a união de todos os
pertence a união de todos os  (com i=1, 2, ..., k), então ele pertence a pelo menos um desses conjuntos.
(com i=1, 2, ..., k), então ele pertence a pelo menos um desses conjuntos.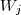 , sendo
, sendo  . Ou seja, suponha que temos
. Ou seja, suponha que temos  .
. , temos que
, temos que  , já que podemos escrever:
, já que podemos escrever: , lembrando que
, lembrando que  com i=1, 2, ..., j-1, j+1, ..., k.
com i=1, 2, ..., j-1, j+1, ..., k.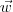 escolhido foi qualquer, podemos concluir que:
escolhido foi qualquer, podemos concluir que:

