 (R)
(R)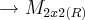
nas bases a={ t, t+2,
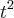 } do
} do 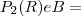
![{\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right], {\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right],](/latexrender/pictures/30224cef379713444b07169de3eb7b7d.png)
![\left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right],](/latexrender/pictures/892179d9a47cb9a55b6029426629014c.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right],](/latexrender/pictures/6bca50fb8ca4c49f3f8141ac14ce9e85.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right],](/latexrender/pictures/4c4c1bb8edd9cefd669f6d47f9527794.png)
![\left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix} \left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix}](/latexrender/pictures/4caa26fdd7e878bc859bc617ed953119.png)
Como faço para encontrar a expressão de T (X,Y)?

 (R)
(R)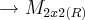
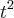 } do
} do 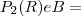
![{\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right], {\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right],](/latexrender/pictures/30224cef379713444b07169de3eb7b7d.png)
![\left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right],](/latexrender/pictures/892179d9a47cb9a55b6029426629014c.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right],](/latexrender/pictures/6bca50fb8ca4c49f3f8141ac14ce9e85.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right],](/latexrender/pictures/4c4c1bb8edd9cefd669f6d47f9527794.png)
![\left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix} \left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix}](/latexrender/pictures/4caa26fdd7e878bc859bc617ed953119.png)

baianinha escreveu:Sabe-se que a matriz de uma transformação linear
é dada por,
considerando as basesde
e
de
.
Encontrar a expressão de T(p).
![[T(p)]_B = [T]_A^B[p]_A [T(p)]_B = [T]_A^B[p]_A](/latexrender/pictures/3a93f5d0d1f92a231aa44c06f4ed5684.png)
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png) - vetor de coordenadas de T(p) na base B;
- vetor de coordenadas de T(p) na base B;![[T]_A^B [T]_A^B](/latexrender/pictures/f6e319aa809880a0d493de6315e37e04.png) - matriz de T em relação as bases A e B;
- matriz de T em relação as bases A e B;![[p]_A [p]_A](/latexrender/pictures/f19f70d560dcff52eeac3ddc1baf38e0.png) - vetor de coordenadas de p na base A;
- vetor de coordenadas de p na base A;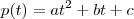 . Nós queremos descobrir os escalares k1, k2 e k3 de modo que
. Nós queremos descobrir os escalares k1, k2 e k3 de modo que 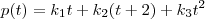 . Arrumando essa equação e comparando os coeficientes dos polinômios, é fácil obter que
. Arrumando essa equação e comparando os coeficientes dos polinômios, é fácil obter que 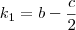 ,
, 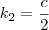 ,
,  . Portanto, temos que:
. Portanto, temos que:![[p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A [p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A](/latexrender/pictures/f45165aaa3dcd73405a55ee2c811ac2e.png)
![[T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B [T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B](/latexrender/pictures/9505de078f9f7005965576b081c636d1.png)
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png) usando o vetor de coordenadas calculado e a base B dada, nós temos:
usando o vetor de coordenadas calculado e a base B dada, nós temos: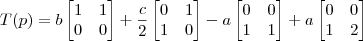
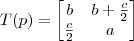

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante