Sejam
 subespaços vetorias .Prove :
subespaços vetorias .Prove :(1) O subespaço gerado pela união
 é o conjunto
é o conjunto  das somas
das somas  ,onde
,onde  .
.OBS.:
Para mostrar que O subespaço gerado pela união
 é subconjunto de
é subconjunto de  mostrei de duas formas que ,são
mostrei de duas formas que ,são  e
e  .A demonstração que
.A demonstração que  é subconjunto do subespaço gerado pela união
é subconjunto do subespaço gerado pela união  encontra-se no item
encontra-se no item  .
. Minha solução :

Seja
 o subespaço gerado pela união
o subespaço gerado pela união  de subespaços de
de subespaços de  .Vamos denotar
.Vamos denotar  por
por  .
. Consideremos
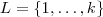 e
e 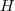 conjunto de índices quaisquer satisfazendo ,
conjunto de índices quaisquer satisfazendo ,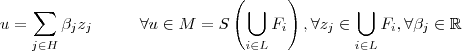 .
. Como
 ,temos que todos seus vetores são combinações lineares dos elementos de
,temos que todos seus vetores são combinações lineares dos elementos de 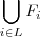 .Em particular , se
.Em particular , se  satisfazendo ,
satisfazendo , 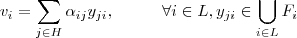 com
com 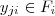 .
.Pela hipótese de
 e
e  serem subespaços de
serem subespaços de  ,obtemos que
,obtemos que  .Assim , tomando-se
.Assim , tomando-se  e
e 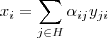 , por
, por 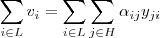 .
. Resulta ,
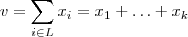 com
com  .
. Assim ,
 .
.  .
.Reciprocamente ,tomando-se
 quaisquer em
quaisquer em  com
com  ,pela hipótese de
,pela hipótese de  gerar
gerar  ,resulta que
,resulta que  .Como estamos trabalhando com vetores genéricos , segue que
.Como estamos trabalhando com vetores genéricos , segue que  .Por
.Por  ,
,  .
. Estou com pouco tempo para postar o item (a_2) .


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.