, definida por T (ax² + bx + c) = c. Ela é injetora e sobrejetora?
A ordem da matriz que representa T em relação às bases canônicas de S4 e B = 1 de
é 1x3?
por barbara-rabello » Ter Nov 20, 2012 14:30
, definida por T (ax² + bx + c) = c. é 1x3?
por MarceloFantini » Ter Nov 20, 2012 15:02
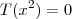mas este polinômio não é identicamente nulo. O que você quer dizer por 
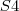? Eu estou assumindo que é o espaço dos polinômios de grau menor ou igual a 2, usualmente denotado por 
.
.
, uma linha e três colunas.
por Ananda » Seg Mar 24, 2008 17:31
por marioitalo » Qua Out 15, 2008 20:26
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.