 por BRUNO2214 » Sex Mar 18, 2016 16:48
por BRUNO2214 » Sex Mar 18, 2016 16:48
Estou tentando resolver exercício
Determine que (v,u) seja LD ,sendo u=(1,m,n+1) e v=(m,n,10).
joguei na matriz que caiu ne um sistema no qual as variáveis :
n-m²=0
10-m(n+1)=0
10m -n(n+1)=0
após isto não sei mais qual rumo tomar !Alguém poderia me ajudar a terminas a fazer e indicar qual matéria eu preciso ter conhecimento para concluir esta equação?
-
BRUNO2214
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Mar 18, 2016 16:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por adauto martins » Seg Mar 21, 2016 19:44
por adauto martins » Seg Mar 21, 2016 19:44
para u,v serem LD,e necessario q. um seja combinaçao do outro,ou seja...
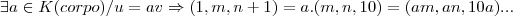
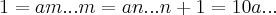
sistema com tres equaçoes e tres incognitas...
faz.as substituiçoes em a,teremos:

,aqui uma eq.de terceiro grau...
ai é determ. o valor de a,depois de m,n...equaçao cubica e calculo,e calculo...
veja metodo de reduçao a uma eq. do tipo...
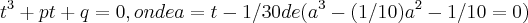
...
bons calculos!resolva-o...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por 0 kelvin » Ter Mar 22, 2016 22:07
por 0 kelvin » Ter Mar 22, 2016 22:07
Se as equações não são lineares, veja se não tem como linearizar com substituição de variável. Veja tb se não tem como cancelar a variável que tem quadrado ou cubo.
Se apareceu um sistema de equações não lineares q não tem jeito com as técnicas comuns pra sistemas lineares, aí ou o enunciado tem erro ou a equação q aparece o termo não linear esta errada.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
Voltar para Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


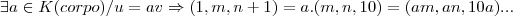
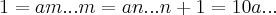 sistema com tres equaçoes e tres incognitas...
sistema com tres equaçoes e tres incognitas... ,aqui uma eq.de terceiro grau...
,aqui uma eq.de terceiro grau...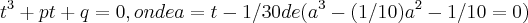 ...
...

