O ESPAÇO É O R3
A SOMA É DEFINIDA POR (X,Y,Z)+(X',Y',Z')=(X+X',Y+Y',Z+Z')
E A MULTIPLICAÇÃO POR K(X,Y,Z)= (KX,Y,Z)
TENTEI FAZER MAS TODOS OS AXIOMAS DERAM CERTO.
TAMBÉM GOSTARIA DE SABER SE O CONJUNTO DE MATRIZES DO TIPO

É ESPAÇO VETORIAL



 . É fácil verificar que a "soma " está bem definida e os axiomas relativos a tal operação estão ok , pode verificar . Agora como o multiplicação por escalar definida de forma não usual é importante ter atenção . Sugiro que check a distributividade , i.e verificar se
. É fácil verificar que a "soma " está bem definida e os axiomas relativos a tal operação estão ok , pode verificar . Agora como o multiplicação por escalar definida de forma não usual é importante ter atenção . Sugiro que check a distributividade , i.e verificar se 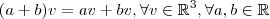 .
.
santhiago escreveu:Como a soma definida é a usual do espaço. É fácil verificar que a "soma " está bem definida e os axiomas relativos a tal operação estão ok , pode verificar . Agora como o multiplicação por escalar definida de forma não usual é importante ter atenção . Sugiro que check a distributividade , i.e verificar se
.
Em relação ao conjunto formado por tal matrizes , pelo que uma de suas entradas é fixa e vale 1 , claramente este conjunto não é munido da matriz nula .

![[ a +b] (x,y,z) = ([a+b] x, y ,c ) [ a +b] (x,y,z) = ([a+b] x, y ,c )](/latexrender/pictures/33781267d33264967ba494b99bcfc51d.png) para quaisquer escalares a,b e vetor v=(x,y,z) pertence ao R^3 . Por outro lado ,
para quaisquer escalares a,b e vetor v=(x,y,z) pertence ao R^3 . Por outro lado , ![a (x,y,z) + b(x,y,z) = (ax,y,z) + (bx,y,z) = (ax + bx , y+ y , z+ z ) = ([a+b]x ,2x ,2z) a (x,y,z) + b(x,y,z) = (ax,y,z) + (bx,y,z) = (ax + bx , y+ y , z+ z ) = ([a+b]x ,2x ,2z)](/latexrender/pictures/c203898fb9425fe889f7b9e80b47a433.png) .
. ![[a +b] v \neq av + bv [a +b] v \neq av + bv](/latexrender/pictures/97d67d19a1ff07a6423a4d29d064c828.png) , ocorrendo a igualdade iff y=z= 0 .
, ocorrendo a igualdade iff y=z= 0 .
santhiago escreveu:Note que pela definição multiplicação por escalar , temos ,para quaisquer escalares a,b e vetor v=(x,y,z) pertence ao R^3 . Por outro lado ,
.
Segue daí que em geral, ocorrendo a igualdade iff y=z= 0 .

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)