
Minha humilde resolucao:





 ;W=(1,0-1) e um ponto do {\Re}^{3}...
;W=(1,0-1) e um ponto do {\Re}^{3}... ,entao:
,entao: ,entao :U+W=(x+1,2x,x),
,entao :U+W=(x+1,2x,x),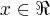
 o q. contradiz pois x=-1 e x=0...logo U+W nao e subespaço do
o q. contradiz pois x=-1 e x=0...logo U+W nao e subespaço do 

 e pelo enunciado
e pelo enunciado 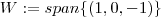 .
. é subespaço do
é subespaço do  e assim um vetor arbitrário deste subespaço é
e assim um vetor arbitrário deste subespaço é 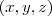 que se exprime como soma de dois vetores
que se exprime como soma de dois vetores  e
e  , e estes vetores são dados por
, e estes vetores são dados por  e
e 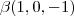 . Segue daí que
. Segue daí que 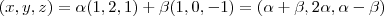 . Logo
. Logo 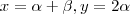 e
e 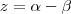 e por isso (soma x + z e substitui 2 alpha por y )
e por isso (soma x + z e substitui 2 alpha por y )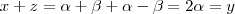 , pedro sua resposta está certa , porém confuso .
, pedro sua resposta está certa , porém confuso .

 a base canônica para o
a base canônica para o  , de acordo com a notação acima
, de acordo com a notação acima ![\mathbb{R}^2 = [\{e_1 , e_2 \} ] \mathbb{R}^2 = [\{e_1 , e_2 \} ]](/latexrender/pictures/eab37dffaff4c2dc5911c50bdb67a424.png) .Eu particularmente evito esta notação e simplesmente escrevo
.Eu particularmente evito esta notação e simplesmente escrevo 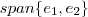 ou
ou  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)