Olá, eu estou em dúvida no seguinte exercício,
Diga quais dos subconjuntos a seguir são subespaços vetoriais. Se não for diga o porquê.
Considere como operações de soma e multiplicação por escalar as usuais de R^n ou M(m,n).
a) X={(x,y,z) E R³; xy=0} está contido em R³
Minha resolução é a seguinte mas não está completa porque eu não consigo terminá-la
Sejam v1=(x1,y1,z1) e v2=(x2,y2,z2) dois vetores arbitrários de X, temos:
v1+v2=(x1,y1,z1)+(x2,y2,z2)=(x1+x2,y1+y2,z1+z2)
Agora testamos se o novo vetor satisfaz a condição que define X, sendo assim, temos,
(x1+x2)*(y1+y2)=x1*y1+x1*y2+x2*y1+x2*y2=0+x1*y2+x2*y1+0=x1y2+x2y1 que é diferente de zero, portanto não é subespaço.
Agora me digam ai se eu fiz errado, se fiz me digam no que errei.


 é subespaço , equivale mostrar que um dos axiomas falham para certo elemento do conjunto X . Por exemplo ,
é subespaço , equivale mostrar que um dos axiomas falham para certo elemento do conjunto X . Por exemplo , 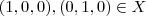 pois
pois  e
e 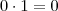 .
.  .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)