![S\neq\left[ \right] S\neq\left[ \right]](/latexrender/pictures/5c19e7b45949d4fb0cbebe538599370b.png) de V, provar que a intersecção
de V, provar que a intersecçãode todos os sub-espaços vetoriais de V que contêm S também é um sub-espaço vetorial
de V, sendo o menor sub-espaço de V que contém S.
Minha tentativa foi basicamente tentar a demonstração através da definição de sub-espaço, ou seja:
Seja W = { W1
 W2...
W2... Wn} a intersecção de todos os sub-espaços vetoriais de V, tal que S
Wn} a intersecção de todos os sub-espaços vetoriais de V, tal que S  W, temos:
W, temos:a) 0
 W, pois por hipotese W é sub-espaço, logo 0
W, pois por hipotese W é sub-espaço, logo 0  S.
S.b) Seja u e v
 W. u + v
W. u + v  W, logo u + v
W, logo u + v  S.
S.c) Seja x

 , e u
, e u  W, logo xu
W, logo xu  W e portanto xu
W e portanto xu  S.
S.Acho que essa demonstração está errada, e não sei como demonstrar que W é o menor sub-espaço de V. Se poderem me ajudar eu agradeço.


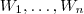 sub-espaços vetoriais de
sub-espaços vetoriais de  os quais contém o subconjunto
os quais contém o subconjunto  de
de 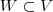 que contém
que contém  será o menor sub-espaço de
será o menor sub-espaço de  .
. é sub-espaço de
é sub-espaço de 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)