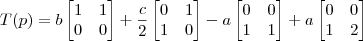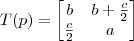por baianinha » Seg Fev 21, 2011 12:59
por baianinha » Seg Fev 21, 2011 12:59
-
baianinha
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qui Dez 16, 2010 12:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Ter Fev 22, 2011 16:44
por LuizAquino » Ter Fev 22, 2011 16:44
baianinha escreveu:Sabe-se que a matriz de uma transformação linear

é dada por
![[T]_A^B = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix} [T]_A^B = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}](/latexrender/pictures/47c2b8e373a3cbbcb8866e0340699d7f.png)
,
considerando as bases
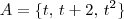
de
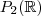
e
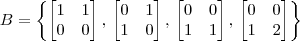
de
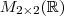
.
Encontrar a expressão de T(p).
Do conhecimento de Álgebra Linear, sabemos que:
![[T(p)]_B = [T]_A^B[p]_A [T(p)]_B = [T]_A^B[p]_A](/latexrender/pictures/3a93f5d0d1f92a231aa44c06f4ed5684.png)
onde
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png)
- vetor de coordenadas de T(p) na base B;
![[T]_A^B [T]_A^B](/latexrender/pictures/f6e319aa809880a0d493de6315e37e04.png)
- matriz de T em relação as bases A e B;
![[p]_A [p]_A](/latexrender/pictures/f19f70d560dcff52eeac3ddc1baf38e0.png)
- vetor de coordenadas de p na base A;
Primeiro, vamos determinar quem é o vetor de coordenadas de p na base A. Sabemos que um polinômio de 2° grau é dado por
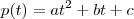
. Nós queremos descobrir os escalares k1, k2 e k3 de modo que
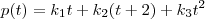
. Arrumando essa equação e comparando os coeficientes dos polinômios, é fácil obter que
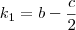
,
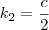
,

. Portanto, temos que:
![[p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A [p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A](/latexrender/pictures/f45165aaa3dcd73405a55ee2c811ac2e.png)
Desse modo, obtemos que:
![[T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B [T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B](/latexrender/pictures/9505de078f9f7005965576b081c636d1.png)
Escrevendo
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png)
usando o vetor de coordenadas calculado e a base B dada, nós temos:
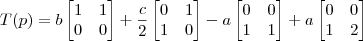
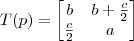
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8150 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10526 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11556 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13597 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9136 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (R)
(R)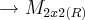
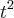 } do
} do 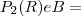
![{\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right], {\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right],](/latexrender/pictures/30224cef379713444b07169de3eb7b7d.png)
![\left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right],](/latexrender/pictures/892179d9a47cb9a55b6029426629014c.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right],](/latexrender/pictures/6bca50fb8ca4c49f3f8141ac14ce9e85.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right],](/latexrender/pictures/4c4c1bb8edd9cefd669f6d47f9527794.png)
![\left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix} \left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix}](/latexrender/pictures/4caa26fdd7e878bc859bc617ed953119.png)

 (R)
(R)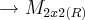
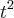 } do
} do 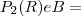
![{\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right], {\left[
\begin{vmatrix}
1 & 1 \\
0 & 0
\end{vmatrix}
\right],](/latexrender/pictures/30224cef379713444b07169de3eb7b7d.png)
![\left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 1 \\
1 & 0
\end{vmatrix}
\right],](/latexrender/pictures/892179d9a47cb9a55b6029426629014c.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 1
\end{vmatrix},}
\right],](/latexrender/pictures/6bca50fb8ca4c49f3f8141ac14ce9e85.png)
![\left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right], \left[
\begin{vmatrix}
0 & 0 \\
1 & 2
\end{vmatrix}
\right],](/latexrender/pictures/4c4c1bb8edd9cefd669f6d47f9527794.png)
![\left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix} \left[T \right]A.B=
\begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1 \\
0 & 0 & 1
\end{pmatrix}](/latexrender/pictures/4caa26fdd7e878bc859bc617ed953119.png)

,
de
e
de
.
![[T(p)]_B = [T]_A^B[p]_A [T(p)]_B = [T]_A^B[p]_A](/latexrender/pictures/3a93f5d0d1f92a231aa44c06f4ed5684.png)
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png) - vetor de coordenadas de T(p) na base B;
- vetor de coordenadas de T(p) na base B;![[T]_A^B [T]_A^B](/latexrender/pictures/f6e319aa809880a0d493de6315e37e04.png) - matriz de T em relação as bases A e B;
- matriz de T em relação as bases A e B;![[p]_A [p]_A](/latexrender/pictures/f19f70d560dcff52eeac3ddc1baf38e0.png) - vetor de coordenadas de p na base A;
- vetor de coordenadas de p na base A;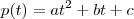 . Nós queremos descobrir os escalares k1, k2 e k3 de modo que
. Nós queremos descobrir os escalares k1, k2 e k3 de modo que 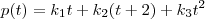 . Arrumando essa equação e comparando os coeficientes dos polinômios, é fácil obter que
. Arrumando essa equação e comparando os coeficientes dos polinômios, é fácil obter que 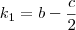 ,
, 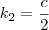 ,
,  . Portanto, temos que:
. Portanto, temos que:![[p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A [p]_A = \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A](/latexrender/pictures/f45165aaa3dcd73405a55ee2c811ac2e.png)
![[T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B [T(p)]_B = [T]_A^B[p]_A = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1 \end{bmatrix}_A^B \begin{bmatrix} b -\frac{c}{2} \\ \frac{c}{2} \\ a \end{bmatrix}_A = \begin{bmatrix} b \\ \frac{c}{2} \\ - a \\ a \end{bmatrix}_B](/latexrender/pictures/9505de078f9f7005965576b081c636d1.png)
![[T(p)]_B [T(p)]_B](/latexrender/pictures/0623fe724e2938dcf2045ddec7cd0665.png) usando o vetor de coordenadas calculado e a base B dada, nós temos:
usando o vetor de coordenadas calculado e a base B dada, nós temos: