 por Claudinei » Dom Out 02, 2011 21:17
por Claudinei » Dom Out 02, 2011 21:17
ENUNCIADO: DOIS CAPITAIS COLOCADOS, O PRIMEIRO, A 4% a.a., DURANTE 8 MESES, E O SEGUNDO, A 3% a.a., DURANTE 9 MESES, RENDEM JUROS IGUAIS. DETERMINAR ESSES CAPITAIS, SABENDO QUE A SUA DIFERENÇA É DE R$ 12,50.
Pv, Pv1 e Pv2 = VALORES PRESENTES
I = JUROS
i = TAXA DE JUROS
n=NÚMERO DE PERÍODOS
I = Pv.i.n/m
TENTATIVA:
Pv1 - Pv2 = 12,50 => Pv1= Pv2 + 12,50
Pv1* 0,04 / 12 * 8 = Pv2 * 0,03/12 * 9
ENTÃO:
RESOLVENDO A SEGUNDA
Pv1 = Pv2 * 0,8427
SUBSTITUINDO NA PRIMEIRA
Pv2 * 0,8427 = Pv2 + 12,50
RESPOSTA Pv2 = R$ 6,78
ONDE ESTÁ O ERRO !?!?!
-
Claudinei
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Out 02, 2011 20:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: FILOSOFIA
- Andamento: formado
 por mausim » Qui Out 27, 2011 11:46
por mausim » Qui Out 27, 2011 11:46
Você fez baseando-se em juros simples?
Vou dar uma volta muito grande, mas espero alcançar o objetivo. Mas vou pelos juros compostos, espero que não lhe cause problemas com isto.
Vamos escrever a sentença, enquanto lemos o enunciado:

que é o mesmo que

Aplicando

Melhorando essa confusão

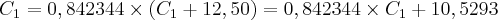


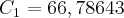
Como
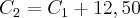
,

Tirando a prova através de
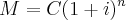
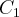
a 4% teremos

Os juros, no caso de
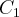
serão

Agora o

a 4% teremos
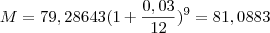
Os juros, no caso de

serão

Ficam assim os juros iguais (1,8018) e os capitais C1 e C2 com a diferença de 12,50.
.
-
mausim
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Out 25, 2011 10:27
- Formação Escolar: SUPLETIVO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Capitalização - Juros Simples e Composto
por abudreis » Qua Set 23, 2015 23:55
- 1 Respostas
- 5707 Exibições
- Última mensagem por nakagumahissao

Sáb Out 03, 2015 10:02
Matemática Financeira
-
- capitalização Simples
por Manoella » Ter Dez 21, 2010 21:32
- 1 Respostas
- 1450 Exibições
- Última mensagem por mausim

Qui Out 27, 2011 10:44
Matemática Financeira
-
- Juros Composto e capitalização.
por ARYANE96 » Ter Abr 14, 2015 19:11
- 0 Respostas
- 2426 Exibições
- Última mensagem por ARYANE96

Ter Abr 14, 2015 19:11
Matemática Financeira
-
- Matemática Financeira - Capitalização Simples
por DidinhoFilho » Seg Jun 27, 2011 14:56
- 1 Respostas
- 1855 Exibições
- Última mensagem por SidneySantos

Ter Jul 19, 2011 21:53
Matemática Financeira
-
- Juros Simples // Juros Compostos
por Roberta » Qui Jul 16, 2009 18:22
- 3 Respostas
- 8206 Exibições
- Última mensagem por Roberta

Qui Jul 16, 2009 19:46
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






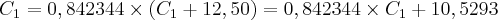


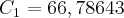
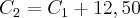 ,
,
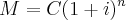
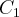 a 4% teremos
a 4% teremos

 a 4% teremos
a 4% teremos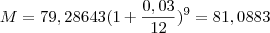




 , avisa que eu resolvo.
, avisa que eu resolvo.

