 por lcsimao » Qua Ago 03, 2011 14:40
por lcsimao » Qua Ago 03, 2011 14:40
Bom dia a todos,
Gosto muito de matemática e sempre tento conseguir fazer coisas novas com ajuda desta
ferramenta. Hávia visitado este site outras vezes para fazer consultas diversas, desta
vez resolvi me cadastrar pois não achei solução para a questão que vou propor. Sei
que o site pede para demostrarmos que tentamos resolver as questões para discuti-las,
em vez de termos só as respostas. Tentei de várias formas resolver o problema abaixo,
mas vou postar somente a última, que de todas a que tentei foi a mais "lúcida".
Segue:
A questão é isolar a variável "i" da equação \[c(\frac{i}{1-(1+i)^{-n}})=pmt\]
Fiz desta forma:
\[c=pmt-pmt\frac{1}{(1+i)^n}\]
\[c=pmt-\frac{pmt}{(1+i)^n}\]
\[c=\frac{pmt(1+i)^n-pmt}{(1+i)^n}\]
e travei aqui...
\[\frac {c(1+i)^n}{pmt}=-1+(1+i)^n\]
tentei fazer logarítmos e tentei encontrar através de raízes, mas sem sucesso.
Agradeço pela ajuda.
-
lcsimao
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Ago 03, 2011 09:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Mecatrônica
- Andamento: cursando
 por lcsimao » Dom Ago 07, 2011 03:53
por lcsimao » Dom Ago 07, 2011 03:53
Pessoal, refiz da forma correta. Espero que agora saia uma ajuda.
Muio grato,
Tenho que isolar
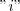
no esquema abaixo:
![\[c(\frac{i}{1-(1+i)^{-n}})=pmt\]
Fiz desta forma:
\[c=pmt-pmt\frac{1}{(1+i)^n}\]
\[c=pmt-\frac{pmt}{(1+i)^n}\]
\[c=\frac{pmt(1+i)^n-pmt}{(1+i)^n}\]
e travei aqui...
\[\frac {c(1+i)^n}{pmt}=-1+(1+i)^n\] \[c(\frac{i}{1-(1+i)^{-n}})=pmt\]
Fiz desta forma:
\[c=pmt-pmt\frac{1}{(1+i)^n}\]
\[c=pmt-\frac{pmt}{(1+i)^n}\]
\[c=\frac{pmt(1+i)^n-pmt}{(1+i)^n}\]
e travei aqui...
\[\frac {c(1+i)^n}{pmt}=-1+(1+i)^n\]](/latexrender/pictures/c32a9ed7bbf1b32cb4a8c6db470e4ea9.png)
-
lcsimao
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Ago 03, 2011 09:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Mecatrônica
- Andamento: cursando
 por lcsimao » Qui Ago 11, 2011 08:36
por lcsimao » Qui Ago 11, 2011 08:36
Bom dia a Todos!!
Ninguém?? Uma só tentativa??
Por favor, há alguém que consiga??
-
lcsimao
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Ago 03, 2011 09:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Mecatrônica
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivado] Isolando Variável
por Niiseek » Seg Out 29, 2012 16:40
- 5 Respostas
- 2567 Exibições
- Última mensagem por Niiseek

Seg Out 29, 2012 17:39
Cálculo: Limites, Derivadas e Integrais
-
- Matematica Financeira - taxa de juros aparente e taxa real
por Patricia estudante » Dom Mai 20, 2012 18:55
- 0 Respostas
- 2321 Exibições
- Última mensagem por Patricia estudante

Dom Mai 20, 2012 18:55
Matemática Financeira
-
- Matematica Financeira - taxa de juros aparente e taxa real
por Patricia estudante » Dom Mai 20, 2012 18:55
- 0 Respostas
- 2299 Exibições
- Última mensagem por Patricia estudante

Dom Mai 20, 2012 18:55
Matemática Financeira
-
- Taxa nominal e Taxa Efetiva
por Danilo Dias Vilela » Qui Out 15, 2009 12:11
- 1 Respostas
- 9864 Exibições
- Última mensagem por marcelo ebm

Ter Nov 24, 2009 22:11
Matemática Financeira
-
- Taxa nominal e Taxa Efetiva
por MuitaGarra » Sáb Mar 24, 2012 11:38
- 1 Respostas
- 2514 Exibições
- Última mensagem por Fabiano Vieira

Dom Abr 22, 2012 18:53
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


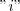
![\[c(\frac{i}{1-(1+i)^{-n}})=pmt\]
Fiz desta forma:
\[c=pmt-pmt\frac{1}{(1+i)^n}\]
\[c=pmt-\frac{pmt}{(1+i)^n}\]
\[c=\frac{pmt(1+i)^n-pmt}{(1+i)^n}\]
e travei aqui...
\[\frac {c(1+i)^n}{pmt}=-1+(1+i)^n\] \[c(\frac{i}{1-(1+i)^{-n}})=pmt\]
Fiz desta forma:
\[c=pmt-pmt\frac{1}{(1+i)^n}\]
\[c=pmt-\frac{pmt}{(1+i)^n}\]
\[c=\frac{pmt(1+i)^n-pmt}{(1+i)^n}\]
e travei aqui...
\[\frac {c(1+i)^n}{pmt}=-1+(1+i)^n\]](/latexrender/pictures/c32a9ed7bbf1b32cb4a8c6db470e4ea9.png)
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.