 por Raphael Feitas10 » Ter Jul 12, 2011 23:53
por Raphael Feitas10 » Ter Jul 12, 2011 23:53
Duas pessoas A e B ganham, num negócio, $ 6600.Sabendo que A deve receber mais 20% de que B,calcule o lucro de A. R:3600
brother essa eu só conseguie interpreta ate aqui
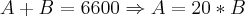
e travei ñ conseguei fazer o resto da questão, me ajuda aew desde ja agredecido.
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Qua Jul 13, 2011 10:15
por FilipeCaceres » Qua Jul 13, 2011 10:15
Basta calcular o seguinte sistema:

Substitua a segunda equação na primeira e resolva.
Se não conseguir poste sua dúvida.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Raphael Feitas10 » Qua Jul 13, 2011 23:41
por Raphael Feitas10 » Qua Jul 13, 2011 23:41
Brother eu substituie mas ñ ahcei essa resposta aew ñ achei 2200 e de onde vc tirou esse 1+2B do enuciado ñ entendie mim ajuda aew desde ja agradecido...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Jul 14, 2011 07:57
por MarceloFantini » Qui Jul 14, 2011 07:57
Um lucro de 20% sobre alguma coisa é matematicamente equivalente a multiplicar por 1,2.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Raphael Feitas10 » Sex Jul 15, 2011 14:07
por Raphael Feitas10 » Sex Jul 15, 2011 14:07
MarceloFantini escreveu:Um lucro de 20% sobre alguma coisa é matematicamente equivalente a multiplicar por 1,2.
Brother eu fiz mais ñ achei a resposta certa me ajuda aew como vc faria essa questão...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sex Jul 15, 2011 18:11
por MarceloFantini » Sex Jul 15, 2011 18:11
Eu montaria o mesmo sistema que o Filipe. Agora é só resolver. Você não sabe? Faça o A na primeira equação igual ao que você tem na segunda, assim terá uma equação só em B, achando seu valor você coloca na segunda equação e terá o lucro de A.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Porcentagem] Fração mista e porcentagem
por Mayra Luna » Ter Fev 26, 2013 20:58
- 2 Respostas
- 4571 Exibições
- Última mensagem por Mayra Luna

Ter Fev 26, 2013 23:41
Álgebra Elementar
-
- Porcentagem - Porcentagem com minutos
por marcorrer » Qua Abr 04, 2012 13:52
- 6 Respostas
- 7886 Exibições
- Última mensagem por marcorrer

Seg Abr 09, 2012 16:25
Álgebra Elementar
-
- Porcentagem
por Danilo Dias Vilela » Qui Set 10, 2009 22:31
- 1 Respostas
- 3743 Exibições
- Última mensagem por Molina

Sex Set 11, 2009 14:22
Matemática Financeira
-
- Porcentagem
por Danilo Dias Vilela » Sex Set 11, 2009 18:09
- 2 Respostas
- 3668 Exibições
- Última mensagem por Danilo Dias Vilela

Sex Set 11, 2009 21:17
Matemática Financeira
-
- Porcentagem
por matematicando » Ter Set 15, 2009 12:52
- 0 Respostas
- 2909 Exibições
- Última mensagem por matematicando

Ter Set 15, 2009 12:52
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
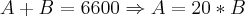 e travei ñ conseguei fazer o resto da questão, me ajuda aew desde ja agredecido.
e travei ñ conseguei fazer o resto da questão, me ajuda aew desde ja agredecido.
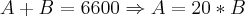 e travei ñ conseguei fazer o resto da questão, me ajuda aew desde ja agredecido.
e travei ñ conseguei fazer o resto da questão, me ajuda aew desde ja agredecido.







